2025 година
Книжка 4
QUALITATIVE EDUCATIONAL PERSPECTIVES ON THE DIVERGENCE AND CONVERGENCE OF SCIENTIFIC THEORY AND PRACTICE
B.H.S. Thimmappa
ОСОБЕНОСТИ В ПРИЛАГАНЕТО НА ИНТЕРДИСЦИПЛИНАРНИЯ ПОДХОД В ОБУЧЕНИЕТО ПО ПРИРОДНИ НАУКИ И ГЕОГРАФИЯ
Цветомир Фавлиянов
ОБОГАТЯВАЩА ПРОГРАМА ЗА ПОДГОТОВКА НА НАДАРЕНИ УЧЕНИЦИ ЗА ОЛИМПИАДИ ПО ХИМИЯ: ПРОЕКТИРАНЕ И РЕАЛИЗАЦИЯ
Борис Толев, Александрия Генджова
ЕКООБРАЗОВАТЕЛНИ ИНТЕРАКТИВНИ ИГРИ
Галя Аралова
CONSTRUCTING AN EXPERIMENTAL EQUIPMENT FOR TESTING THE INFLUENCE OF NATURAL GAS – HYDROGEN MIXTURE ON THE PRODUCTION TUBING
Veselin Mitkov
NEW TECHNOLOGY FOR DEVELOPING HYDROCARBON RESERVES OF COMPLEX RESERVOIRS WITH UNDERLYING WATER
Miel Hofmann, Sudad H. Al-Obaidi, Igor P. Kamensky
Книжка 3
ПРАЗНИК НА ХИМИЯТА 2025
Александра Камушева, Златина Златанова
ФАТАЛНИЯТ 13
Гинчо Гичев, Росица Стефанова
ХИМИЯТА НА БАНКНОТИТЕ И МОНЕТИТЕ – НАПРЕДЪКЪТ НА НАУКАТА
Джемал Камберов, Фатиме Хюсеин
ХИМИЯ НА БАНКНОТИТЕ И МОНЕТИТЕ ОТ ВРЕМЕТО НА НАШИТЕ ПРА-, ПРАРОДИТЕЛИ ДО ДНЕС
Ибрахим Мисанков, Фатиме Хюсеин
ХИМИЯ НА МЕДОВИНАТА
Габриела Иванова, Галя Аралова-Атанасова
Х ИМ ИЯ НА Б АНКНОТИТЕ И МОНЕТИТЕ
Ивайло Борисов, Мая Ганева
АЛУМИНИЙ – „ЩАСТЛИВИЯТ“ 13-И ЕЛЕМЕНТ
Мария Кирилова, Ралица Ранчова
МЕТАЛЪТ НА ВРЕМЕТО
Християна Христова, Мария Стойнова
СЛАДКА ЛИ Е ФРЕНСКАТА ЛУЧЕНА СУПА?
Женя Петрова, Мими Димова
АЛУМИНИЯТ – ЛЕКИЯТ „ЗДРАВЕНЯК“ В АВТОМОБИЛОСТРОЕНЕТО
Миа Бъзовска, Мадлена Колчева
ПАРИТЕ – ИСТОРИЯ И НЕОБХОДИМОСТ
Мария Александрова, Румяна Стойнева
ХИМИЯ НА ХАРТИЕНИТЕ БАНКНОТИ – АМЕРИКАНСКИ ДОЛАР
Йоан Хашъмов, Даниела Баева
АЛУМИНИЯТ – ОТ ОТПАДЪК ДО РЕСУРС
Стилян Атанасов, Никола Иванов, Галина Кирова
МЕТАЛЪТ ИЗЯЩЕСТВО: АЛУМИНИЯТ В СЪВРЕМЕННАТА БИЖУТЕРИЯ
Верка Поповска, Русанка Петрова
ТАЙНАТА ХИМИЯ НА ШВЕЙЦАРСКИТЕ БАНКНОТИ
Ивайла Николова, Марияна Георгиева
ХИМИЯТА – ДЕТЕКТИВ ИЛИ ПРЕСТЪПНИК?
Алвина Илин, Валентина Ткачова, Петя Петрова
БЕБЕШКИ ШАМПОАН ОТ ЯДЛИВИ СЪСТАВКИ: ФОРМУЛИРАНЕ НА НОВ КОЗМЕТИЧЕН ПРОДУКТ
Хана Крипендорф, 5, Даниел Кунев, 5, Цветелина Стоянова
БЪЛГАРСКОТО ИМЕ НА ДЪЛГОЛЕТИЕТО
Сияна Краишникова, Анелия Иванова
ХИМИЯ НА МОНЕТИТЕ
Кристина Анкова, Сияна Христова, Ростислава Цанева
ХИМИЯ НА ШОКОЛАДА
Камелия Вунчева, Мария-Сара Мандил, Марияна Георгиева
ХИМИЯТА НА ПАРИТЕ
Биляна Куртева, Ралица Ранчова
АЛУМИНИЯТ В КРИОГЕНИКАТА
Даниел Анков, Ива Петкова, Марияна Георгиева
ПРИЛОЖЕНИЕ НА АЛУМИНИЯ ВЪВ ВАКСИНИТЕ
Станислав Милчев, Петя Вълкова
АЛУМИНИЙ: „КРИЛА НА ЧОВЕЧЕСТВОТО – ЛЮБИМЕЦ 13“
Ростислав Стойков, Пепа Георгиева
ХИМИЯТА В ПЧЕЛНИЯ МЕД
Сиана Каракашева, Симона Тричкова, Майя Найденова-Георгиева
ИЗПОЛЗВАНЕ НА АЛУМИНИЙ В БИЖУТЕРИЯТА: БИЖУТА ОТ АЛУМИНИЕВА ТЕЛ
Талиса Якимова, Галя Аралова-Атанасова
ХИМИЯ НА МЛЕЧНИТЕ ПРОДУКТИ
Пламена Боиклиева, 10 клас, Дафинка Юрчиева
ХИМИЯ В МАСЛИНИТЕ
Симона Гочева, Майя Найденова
ХИМИЯ НА ЛЮТОТО
Марта Пенчева, Васка Сотирова
ХИНАП – ИЗСЛЕДВАНЕ НА СЪДЪРЖАНИЕТО НА ВИТАМИН С
Елица Нейкова, Елисавета Григорова, Майя Найденова
АЛУМИНИЯТ – ЧУДНИЯТ МЕТАЛ, ОФОРМИЛ СЪВРЕМЕННАТА ЦИВИЛИЗАЦИЯ
Живко Зидаров, Деян Димчев
ХИМИЯ НA ПAРИТE
Игликa Кoлeвa, Eмилия Ивaнoвa
ВЛИЯНИЕ НА МАРИНАТИТЕ ВЪРХУ МЕСОТО
Емил Мирчев, Галя Петрова
АНАЛИЗ НА ПРИРОДНИ ВОДИ В ОБЩИНА СЛИВЕН
Никола Урумов, Анелия Иванова
МОГАТ ЛИ ТЕСТОВЕТЕ В ДОМАШНИ УСЛОВИЯ НАДЕЖДНО ДА ОПРЕДЕЛЯТ КАЧЕСТВОТО И АВТЕНТИЧНОСТТА НА МЕДА?
Ева-Мария Дръндарова, Елисавета Митова
ТРИНАДЕСЕТИЯТ ЕЛЕМЕНТ – СПАСИТЕЛ ИЛИ ТИХ РАЗРУШИТЕЛ?
Виктория Дечкова, Никола Велчев, Нели Иванова
Книжка 2
A CONCEPT MAP DESIGN FOR IDENTIFICATION AND CORRECTION OF STUDENTS’ MISCONCEPTIONS ABOUT WAVE-PARTICLE DUALITY OF LIGHT
Ekaterina S. Pisanova, Zhelyazka D. Raykova, Nina Gereva
„ОТКРИВАНЕТО НА НОВИ НЕЩА Е ВАЖНО“: ВЛИЯНИЕ НА САМОСТОЯТЕЛНАТА ДЕЙНОСТ В КЛАС ВЪРХУ НАГЛАСИТЕ ЗА УЧЕНЕ ПО ХИМИЯ В ГИМНАЗИЯТА
Мартина Евгениева, Милена Кирова
ПРОБЛЕМНО И ПРОЕКТНО БАЗИРАНО ОБУЧЕНИЕ В РАМКИТЕ НА ИЗВЪНКЛАСНА ДЕЙНОСТ „СВЕТЛИНАТА, БЕЗ КОЯТО НЕ МОЖЕМ – ПРОБЛЕМИ И РЕШЕНИЯ“
Стойна Илиева
ЕМОЦИОНАЛНАТА ИНТЕЛИГЕНТНОСТ КАТО ФАКТОР ЗА УСПЕШНА РЕАЛИЗАЦИЯ НА ПЕДАГОЗИ – БЪДЕЩИ УЧИТЕЛИ ПО БИОЛОГИЯ
Клаида Дойчинова
NEW TECHNOLOGIES TO INVESTIGATE THE BEHAVIOUR OF SILICA GELS IN POROUS MEDIA
Sudad H. Al-Obaidi, Miel Hofmann
Книжка 1
ПРОУЧВАНЕ НА ПОДХОДИТЕ КЪМ УЧЕНЕТО НА СТУДЕНТИ ПО ХИМИЯ И ФАРМАЦИЯ
Христо Христов, Александрия Генджова
ДИГИТАЛНИ РЕСУРСИ ЗА РАЗВИТИЕ НА КЛЮЧОВИ КОМПЕТЕНТНОСТИ ПРИ ИЗУЧАВАНЕ НА ХАРАКТЕРИСТИКИТЕ НА ХИМИЧНИТЕ ПРОЦЕСИ В X КЛАС
Мартина Ценова
PERSPECTIVES ON FOOD WASTE MANAGEMENT AND THE GREEN FOOD MOVEMENT
B.H.S. Thimmappa
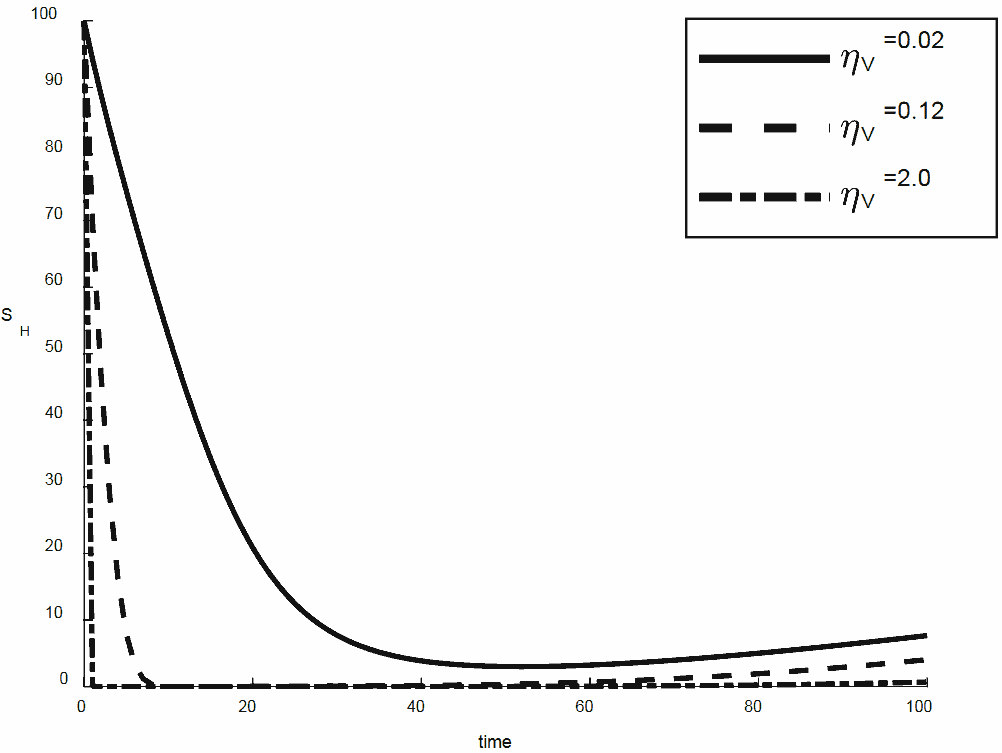
MATHEMATICAL MODELLING OF THE TRANSMISSION DYNAMICS OF PNEUMONIA AND MENINGITIS COINFECTION WITH VACCINATION
Deborah O. Daniel, Sefiu A. Onitilo, Omolade B. Benjamin, Ayoola A. Olasunkanmi
2024 година
Книжка 5-6
ЕЗИКОВА КОМПЕТЕНТНОСТ И КОМПЕТЕНТНОСТ НА УЧЕНИЦИТЕ ЗА ЗДРАВОСЛОВЕН НАЧИН НА ЖИВОТ – ПИЛОТНО ДИАГНОСТИЧНО ИЗСЛЕДВАНЕ В ПЪРВИ ГИМНАЗИАЛЕН ЕТАП
Надежда Райчева, Виолета Вълчева-Славчева
ПРОУЧВАНЕ НА ПЕДАГОГИЧЕСКОТО МНЕНИЕ ПО ОТНОШЕНИЕ НА ЕКОЛОГИЧНОТО ОБРАЗОВАНИЕ В ИЗВЪНКЛАСНА И ИЗВЪНУЧИЛИЩНА СРЕДА
Милка Асенова
ТЕСТОВ ИНСТРУМЕНТАРИУМ ЗА ДИАГНОСТИКА НА ГРАФИЧНИТЕ ЗНАНИЯ И УМЕНИЯ НА УЧЕНИЦИТЕ В ОБУЧЕНИЕТО ПО ХИМИЯ
Антоанета Ангелачева
ИЗПОЛЗВАНЕ НА ЗАДАЧИ В КОНТЕКСТ ПО ТЕМАТА „ПРИРОДНИ ИЗТОЧНИЦИ НА ВЪГЛЕВОДОРОДИ“ ЗА НАСЪРЧАВАНЕ НА КРИТИЧНОТО МИСЛЕНЕ НА УЧЕНИЦИТЕ<span> \(\(^1\)\) </span>
Весела Павлова, Александрия Генджова
A STUDY ON HOW PERMEABILITY HETEROGENEITY INFLUENCES INITIAL WATER CUT IN UNDERSATURATED OIL FORMATIONS
Sudad H. Al-Obaidi, Meil Hofmann, Ivan P. Kamensky
ДОБРИ ПРАКТИКИ В ОБУЧЕНИЕТО ПО ПРИРОДНА ГЕОГРАФИЯ
Георги Марков
ПТИЦИТЕ В СРЕДНОВЕКОВНОТО БЪЛГАРСКО ИЗКУСТВО
Златозар Боев
ИЗГУБЕНИТЕ ЛЕКАРСТВА: МАРИН ЖЕЧЕВ – ЖИВОТ И ТВОРЧЕСТВО
Даниела Начева
Книжка 3-4
НАГЛАСИ НА УЧЕНИЦИТЕ ЗА УЧЕНЕ ПО ХИМИЯ: ХАРАКТЕРИСТИКИ, ФАКТОРИ И ИНСТРУМЕНТИ ЗА ИЗСЛЕДВАНЕ
Мартина Евгениева
ВИДЕОЕКСПЕРИМЕНТЪТ В ОБУЧЕНИЕТО: МОДЕЛ ЗА ПРИЛОЖЕНИЕТО МУ ПРИ ИЗУЧАВАНЕ НА ХИМИЯ И ОПАЗВАНЕ НА ОКОЛНАТА СРЕДА
Йорданка Стефанова, Стоянка Николова, Десислава Иванова
STEM ОБРАЗОВАНИЕ: ПОДОБРЯВАНЕ НА КОМПЕТЕНТНОСТИТЕ НА УЧЕНИЦИТЕ ЧРЕЗ ИНОВАЦИИ В УРОКА „ХРАНЕНЕ И ЗДРАВЕ“ В V КЛАС
Дамяна Грънчарова, Сануш Лапандова
TEACHING FOR A SUSTAINABLE FUTURE: CASE STUDIES FROM THE GREEN SCHOOLS PROJECT IN BULGARIA
Lachezar Afrikanov
РОЛЯТА НА УНИВЕРСИТЕТСКАТА БОТАНИЧЕСКА ГРАДИНА – СОФИЯ, ЗА ПОПУЛЯРИЗИРАНЕ И ИЗУЧАВАНЕ НА РАСТИТЕЛНОТО БИОРАЗНООБРАЗИЕ
Юлияна Атанасова
EVALUATING THE EFFICACY OF WATER ALTERNATING GAS INJECTION TECHNIQUE IN THE UPPER JURASSIC HYDROCARBON RESERVOIRS, CONSIDERING SATURATION PRESSURE
Meil Hofmann, Sudad H. Al-Obaidi, Wang J. Chang
Книжка 1-2
ПОСТАВЯНЕ НА УЧЕНИЦИТЕ В ЦЕНТЪРА НА УЧЕБНИЯ ПРОЦЕС ЧРЕЗ ИЗПОЛЗВАНЕ НА STEAM ПРОЕКТНО БАЗИРАНО ОБУЧЕНИЕ В ПРОГИМНАЗИАЛЕН ЕТАП НА ОБУЧЕНИЕ – МЕТОДИЧЕСКИ НАСОКИ ЗА УЧИТЕЛИ
Станислава Йорданова
УРОЦИ ЗА УНИВЕРСИТЕТСКОТО ОБРАЗОВАНИЕ – КАКВО Е ПОЛЕЗНО ДА ЗАИМСТВА ОТ УЧИЛИЩНОТО?
Катерина Сакалийска
ВЪЗМОЖНОСТИ ЗА НЕФОРМАЛНО ЕКОЛОГИЧНО ОБУЧЕНИЕ ЧРЕЗ ОБРАЗОВАТЕЛНА ПРОГРАМА „ОКОЛНА СРЕДА“
Милка Асенова
STEM МАТЕМАТИЧЕСКО АТЕЛИЕ ЗА МАЛКИ И ГОЛЕМИ В ОБУЧЕНИЕТО ПО МАТЕМАТИКА В ПОДГОТВИТЕЛНА ГРУПА НА ДЕТСКАТА ГРАДИНА
Пенка Борисова
ПРИЛОЖЕНИЕ НА ГРАФИЧНИТЕ ЗАДАЧИ В ОБУЧЕНИЕТО ПО ХИМИЯ
Антоанета Ангелачева
OFFSHORE HEAVY OIL DISPLACEMENT USING WATER FLOODING: FLOW CHARACTERISTICS AND EFFICIENCY
Sudad H. Al-Obaidi, Wang J. Chang, Falah H. Khalaf
2023 година
Книжка 5-6
ПРИРОДОНАУЧНАТА ГРАМОТНОСТ В ДЪРЖАВНИТЕ ОБРАЗОВАТЕЛНИ СТАНДАРТИ В БЪЛГАРИЯ (ПРОГИМНАЗИАЛЕН ЕТАП)
Теодора Коларова, Иса Хаджиали
ТРУДНОСТИ И ПОГРЕШНИ СХВАЩАНИЯ НА БЪЛГАРСКИ УЧЕНИЦИ ПРИ ИЗУЧАВАНЕТО НА ХИМИЧНА КИНЕТИКА
Мартина Ценова
ИЗПОЛЗВАНЕ НА КОНТЕКСТ В ОБУЧЕНИЕТО ПО ХИМИЯ ЗА АНГАЖИРАНОСТ НА УЧЕНИЦИТЕ ОТ IX КЛАС ПО ТЕМА „ЕДНОВАЛЕНТНИ АЛКОХОЛИ“
Весела Павлова
ПОДКАСТ – КОГА, АКО НЕ СЕГА?
Христо Чукурлиев
ЖИВОТ, ПОСВЕТЕН НА НАУКАТА. 100 ГОДИНИ ОТ РОЖДЕНИЕТО НА ПРОФ. Д.Х.Н. ЕЛЕНА КИРКОВА
Димитър Тодоровски, Мария Миланова
Книжка 3-4
DEVELOPMENT OF OIL FIELDS USING SCIENCE ARTIFICIAL INTELLIGENCE AND MACHINE LEARNING
Al-Obaidi S.H., Chang W.J., Hofmann M.
AGILE SOFTWARE DEVELOPMENT ASSISTED IMPLEMENTATION OF A MENTORING SOLUTION IN A LARGE ENTERPRISE
Vladislav Yurukov
БЪЛГАРСКИ НАРОДНИ ПРОТИВОПРИРОДНИ ОБИЧАИ И СУЕВЕРИЯ
Златозар Боев
РАЗВИВАНЕ НА ЗДРАВНО-ЕКОЛОГИЧНИ КОМПЕТЕНТНОСТИ В ОБУЧЕНИЕТО ПО ХИМИЯ ЧРЕЗ СИСТЕМА ОТ УЧЕБНИ ЗАДАЧИ
Антоанета Ангелачева, Станислава Стефанова
INTEGRATING PRIMARY SOURCE ANALYSIS IN REMOTE TEACHING OF EARTH AND ENVIRONMENTAL SCIENCE DURING THE COVID-19 PANDEMIC
Irina Kopteva
MODELLING THE IMPACT OF VACCINATION ON THE TRANSMISSION DYNAMICS OF COVID-19 IN THE PRESENCE OF ENVIRONMENTAL FACTOR
Deborah O. Daniel, Shola A. Akinboboye
Книжка 2
ENHANCED OIL RECOVERY IN TERRIGENOUS OIL FIELDS USING LOW-SALT WATER
Al-Obaidi S.H., Hofmann M., Khalaf F.H.
ЛЕСЕН ЕКСПЕРИМЕНТ ЗА ТРУДНИ КОНЦЕПЦИИ. ПОСТРОЯВАНЕ НА КАЛИБРАЦИОННА КРИВА И ЙОДОМЕТРИЯ
Наско Стаменов
СРАВНИТЕЛЕН АНАЛИЗ НА МЕНТАЛНИ МОДЕЛИ И ИЗКУСТВЕН ИНТЕЛЕКТ
Пламен Чергаров
Книжка 1
EVALUATION OF QUANTITATIVE CRITERIA FOR TRIASSIC RESERVOIRS IN THE SOUTH MANGYSHLAK BASIN
Hofmann, M., AL-Obaidi, S. H., Chang W. J.
REVIEW OF THE DEVASTATING SERIES OF EARTHQUAKES IN TÜRKIYE AND SYRIA IN FEBRUARY 2023. EARTHQUAKE ANALISYS USING SAR SATELLITE DATA: PRELIMINARY RESULTS
Irina Gancheva, Lyuba Dimova
ПРИРОДОНАУЧНОТО ОБРАЗОВАНИЕ В БЪЛГАРИЯ И ДЕСЕТТЕ ТОП НОВОВЪЗНИКНАЛИ ТЕХНОЛОГИИ 2019 – 2021 В ОБЛАСТТА НА ХИМИЯТА
Христо Христов
ТРУДНОСТИ НА УЧЕНИЦИТЕ ПРИ ИЗУЧАВАНЕ НА ОРГАНИЧНА ХИМИЯ НА БАЗОВО НИВО В IX КЛАС
Александрия Генджова, Калин Чакъров
2022 година
Книжка 6
A REVIEW OF MORTALITY ANALYSES AND LIFE SAFETY IN AN INDIAN CONTEXT
B. H. S. Thimmappa
METEOROLOGICAL DETERMINANTS OF COVID-19 DISEASE: A LITERATURE REVIEW
Z. Mateeva, E. Batchvarova, Z. Spasova, I. Ivanov, B. Kazakov, S. Matev, A. Simidchiev, A. Kitev
Книжка 5
IMPROVEMENT OF OIL RECOVERY IN HYDROCARBON FIELDS BY DEVELOPING POLYMERIC GEL-FORMING COMPOSITION
AL-Obaidi S.H., Hofmann M., Smirnova V.
MATHEMATICAL MODELLING OF THE TRANSMISSION MECHANISM OF PLAMODIUM FALCIPARUM
Onitilo S. A, Usman M. A., Daniel D. O. Odetunde O. S., Ogunwobi Z. O., Hammed F. A., Olubanwo O. O., Ajani A. S., Sanusi A. S., Haruna A. H.
INCORPORATION OF NATURE’S DESIGN AND DEVELOPMENT IN HIGHER SCIENCE EDUCATION CURRICULUM DESIGN AND RESEARCH PRACTICE
B. Shivamurthy, B.H.S. Thimmappa2)
ПОСТАНОВКА ЗА ИЗМЕРВАНЕ СКОРОСТТА НА ЗВУКА ВЪВ ВЪЗДУХ
Станислав Сланев, Хафизе Шабан, Шебнем Шабан, Анета Маринова
Книжка 4
MAGNETIC PROPERTIES
Sofija Blagojević, Lana Vujanović, Andreana Kovačević Ćurić
AN EVALUATION OF WATER AND GAS INJECTIONS WITH HYDRAULIC FRACTURING AND HORIZONTAL WELLS IN OIL-SATURATED SHALE FORMATIONS
Al-Obaidi S. H., Kamensky I. P., Hofmann M., Khalaf F. H.
„TAP, TAP WATER“ QUANTUM TUNNELING DEMONSTRATION
Katarina Borković, Andreana Kovačević Ćurić
Книжка 3
IS IT SIMPLE TO EXPLAIN THE SIMPLE EXPERIMENTS? HOW DO SOLID BODIES FLOAT?
Dragia Ivanov, Stefan Nikolov
НАЙ-ГОЛЕМИЯТ СИМПОЗИУМ ЗА НАУКИ ЗА ЗЕМЯТА В ЕВРОПА ПРЕЗ ПОГЛЕДА НА ЕДИН СТУДЕНТ
Драгомир Драгомиров
ВЪЗМОЖНОСТИ НА УЧЕБНИЯ ЕКСПЕРИМЕНТ ЗА ФОРМИРАНЕ НА ПРИРОДОНАУЧНА ГРАМОТНОСТ НА СТУДЕНТИТЕ – БЪДЕЩИ УЧИТЕЛИ ПО ХИМИЯ
Антоанета Ангелачева
MODELLING THE DEVELOPMENT OF OIL RIM USING WATER AND GAS INJECTION
Al-Obaidi S.H., Chang Wj., Hofmann M.
Книжка 2
КОМЕТИТЕ – I ЧАСТ
Пенчо Маркишки
ANALOGIES BETWEEN CHEMICAL REACTIONS AND QUALITY OF WORKPLACE ENVIRONMENT
Àngel Berna, Gonzalo Miranda
ИЗСЛЕДВАНЕ ПОВЕДЕНИЕТО НА КОНИЧНИ КУПЧИНИ ОТ ГРАНУЛИ И ПРАХ
Драгни Драгнев
Книжка 1
ОТ ЛУКА ДО ЛЕКА И ДО РОДОСЛОВНОТО ДЪРВО НА ЖИВОТА
Здравка Костова
МЕТЕОРИ. ОСНОВНИ ПОНЯТИЯ И ТЕРМИНОЛОГИЯ – II ЧАСТ
Валентин Велков
СРАВНЕНИЕ НА ФОРМАТИТЕ НА ДЗИ ЗА ПРОФИЛИРАНА ПОДГОТОВКА ПО ИЗБРАНИ МАТУРИТЕТНИ ПРЕДМЕТИ И ПРОГНОЗА ЗА ОЧАКВАНИТЕ РЕЗУЛТАТИ ОТ ТЯХ
Иван Дреновски
РЕЗУЛТАТИ ОТ ВЪНШНОТО ОЦЕНЯВАНЕ ПО БИОЛОГИЯ И ЗДРАВНО ОБРАЗОВАНИЕ – VIII КЛАС (2018/2019 Г.)
Светла Буковска, , Иса Хаджиали
DISTANCE LEARNING: HOMEMADE COLLOIDAL SILVER
Ana Sofía Covarrubias-Montero, Jorge G. Ibanez
2021 година
Книжка 6
STUDY OF COMPOSITIONS FOR SELECTIVE WATER ISOLATION IN GAS WELLS
Al-Obaidi S.H., Hofmann M., Smirnov V.I., Khalaf F.H., Alwan H.H.
МУТАЦИИ И ВАРИАНТИ НА КОРОНАВИРУСА SARS-COV-2, ПРИЧИНИТЕЛ НА COVID-19
Лъчезар Карагьозов
SEMIEMPIRICAL QUANTUM CHEMICAL AND AB INTIO STUDY OF Co(II), Ni(II),Cu(II) AND Zn(II) COMPLEXES WITH THE AZO DYE DERIVED FROM 4-AMINO ANTIPYRINE AND 2,4-DIHYDROXY ACETOPHEONE
Satya Narayan Chaulia
ON THE SOUND, PRODUCED BY A COIN, ROLLING IN A BALLOON
Denitsa Vasileva
ТРУДНИ ТЕМИ В УЧЕБНАТА ПРОГРАМА ПО ХИМИЯ ОТ ГЛЕДНА ТОЧКА НА УЧЕНИЦИТЕ
Калин Чакъров, Александрия Генджова
Книжка 5
POTENTIAL APPLICATIONS OF ANTIBACTERIAL COMPOUNDS IN EDIBLE COATING AS FISH PRESERVATIVE
Maulidan Firdaus, Desy Nila Rahmana, Diah Fitri Carolina, Nisrina Rahma Firdausi, Zulfaa Afiifah, Berlian Ayu Rismawati Sugiarto
MOLECULAR MODEL AND ITS SIMPLIFICATION IN TEACHING STEREOISOMERISM AT UNDERGRADUATE LEVEL
Girija Shankar Singh
МЕТЕОРИ. OСНОВНИ ПОНЯТИЯ И ТЕРМИНОЛОГИЯ
Валентин Велков
ОТ ОБРАЗУВАНЕТО НА ЗЕМЯТА ДО УСТАНОВЯВАНЕТО НА ЛУКА
Здравка Костова
1300 ГОДИНИ ОТ РОЖДЕНИЕТО НА ГЕБЕР – УЧЕНИЯТ НАЧАЛО И ФУНДАМЕНТ НА АРАБСКАТА АЛХИМИЯ
Нано Рангелов Степанов
Книжка 4
ON THE SYNCHRONIZATION OF CANDLE OSCILLATORS
Yavor Yordanov
ANALYSIS OF THE LIQUIDS COMPOSITION BY THE SOUND PRODUCED BY THEIR HEATING
Grigori Matein, Asen Pashov
CALCULATION METHOD FOR DETERMINING THE GAS FLOW RATE NEEDED FOR LIQUID REMOVAL FROM THE BOTTOM OF THE WELLBORE
Hofmann M., AL-Obaidi S.H., Kamensky I.P.
Книжка 3
GENERATION OF NO2 BY LEAD NITRATE PYROLYSIS: NEVER DO MODIFICATIONS A PRIMA VISTA
Vladimir M. Petruševski
COMPUTATIONAL ANALYSIS OF THE MESSENGER RNA VARIANTS ENCODING TWO ISOFORMS OF THE HIGH-MOBILITY GROUP BOX 1 PROTEIN
Luchezar Karagyozov, Jordana Todorova
PROFESSIONAL DISPOSITIONS OF GRADUATE PRE-SERVICE MATHEMATICS TEACHERS AMONG THREE COLLEGE OF TEACHER EDUCATION IN ETHIOPIA
Anteneh Tefera, Mulugeta Atnafu, Kassa Michael
ОСНОВНИ ДИДАКТИЧЕСКИ АСПЕКТИ, СВЪРЗАНИ С ПРИЛАГАНЕ НА STEM ТЕХНОЛОГИЯТА В ОБУЧЕНИЕТО ПО ПРИРОДНИ НАУКИ
Христина Петрова
РАЗВИТИЕ НА ХИПОТЕЗИТЕ ЗА БИОХИМИЧНИЯ ПРОИЗХОД НА ЖИВОТА
д.п.н Здравка Костова
Книжка 2
INVESTIGATION OF 238U, 234U AND 210PO CONTENT IN SELECTED BULGARIAN DRINKING WATER
Bozhidar Slavchev, Elena Geleva, Blagorodka Veleva, Hristo Protohristov, Lyuben Dobrev, Desislava Dimitrova, Vladimir Bashev, Dimitar Tonev
РЕФЛЕКСИВНОТО УМЕНИЕ – КОНСТРУКТИВНО-ПРОГНОСТИЧЕН АНАЛИЗ В МЕТОДИЧЕСКИ КОНТЕКСТ
Наташа Цанова, Надежда Райчева, Иса Хаджиали
МЕТОДОЛОГИЧНА РАМКА ЗА ИЗВЕЖДАНЕ НА СМИСЛООБРАЗУВАЩИ КАТЕГОРИИ В МЕТОДИКАТА НА ОБУЧЕНИЕ ПО БИОЛОГИЯ
Надежда Райчева
ПЪРВИ СТЪПКИ В КВАНТОВАТА ФИЗИКА ЕЛЕМЕНТАРНО ИЗЛОЖЕНИЕ II. МОДЕЛНИ ПРИМЕРИ (ПОТЕНЦИАЛНИ ЯМИ)
Михаил Аврамов, Димитър Мърваков
Книжка 1
REVEAL THE POTENCY OF WATER HYACINTH AND RED GINGER EXTRACT AS HYDROGEL WOUND DRESSING FOR MRSA DIABETIC WOUND: A SHORT REVIEW
Maulidan Firdaus, Muhammad Iqbal Daniswara, Khoirul Jamaluddin, Novi Andriani
DEMONSTRATION OF DAMPED ELECTRICAL OSCILLATIONS
Elena Grebenakova, Stojan Manolev
ALIGNMENT OF ETHIOPIAN PRIMARY SCHOOL PRE-SERVICE TEACHER EDUCATION PROGRAM WITH THAT PRIMARY SCHOOL MATHEMATICS CONTENTS/SYLLABI
Anteneh Tefera, Mulugeta Atnafu, Kassa Michael
2020 година
Книжка 6
EYE COLOUR INHERITANCE IN HUMANS
Viktor Gilin
THE SUCCESSFUL TURNOVER OF PHOTOSYSTEM II CORE COMPLEXES USING LASER FLASH ILLUMINATION
Bernard Baituti
USING MOLECULAR MODELS TO NAME AND ILLUSTRATE STRUCTURES OF MONOCYCLIC COMPOUNDS
Claudia Quayson, Ruby Hanson
ИНТЕГРИРАНЕ НА ОНЛАЙН РЕСУРСИ НА ТЕМА АСТРОБИОЛОГИЯ В ОБУЧЕНИЕТО ПО АСТРОНОМИЯ В ГИМНАЗИАЛЕН ЕТАП НА СРЕДНАТА СТЕПЕН НА ОБРАЗОВАНИЕ
Десислава Антонова, Владимир Божилов
ДОЦ. Д-Р МАРЧЕЛ КОСТОВ КОСТОВ ЖИВОТ И ТВОРЧЕСТВО
Здравка Костова, Елена Георгиева
Книжка 5
ИЗСЛЕДВАНИЯ ВЪРХУ ЗАРАЖДАНЕТО И РАСТЕЖА НА КРИСТАЛИТЕ
Христо Н. Нанев
ON THE STRUCTURE AND EVOLUTION OF TWO-DIMENSIONAL SOAP FOAM, ENCLOSED BETWEEN GLASS SHEETS
Yavor Yordanov
APPLIED SAMPLING METHODOLOGY AND ANALYSIS OF NONLINEAR ACOUSTIC PROPERTIES IN SOLIDS OF REVOLUTION
G.I. Ivanov
MULTIPLE PERSPECTIVES ON ACADEMIC LABORATORY SAFETY COURSE IN COLLEGE SCIENCE EDUCATION
B.H.S. Thimmappa
ТЕАТЪР НА ФИЗИКАТА ИЛИ ФИЗИКА В ТЕАТЪРА?
Радка Костадинова
Книжка 4
TEACHING PHASES OF THE MOON WITH A ROLE PLAY
Mehmet Karakaş
МОДЕЛ ЗА ИЗПОЛЗВАНЕ НА ОБЛАЧНИТЕ ТЕХНОЛОГИИ В ИНТЕРДИСЦИПЛИНАРЕН ПРОЕКТ ПО ХИМИЯ И ОПАЗВАНЕ НА ОКОЛНАТА СРЕДА
Калина Иванова
СРАВНЕНИЕ НА ИНТЕРАКТИВНИ МЕТОДИ ЗА ОБУЧЕНИЕ ПО ФИЗИКА И АСТРОНОМИЯ В Х КЛАС, I РАВНИЩЕ
Нина Атанасова Танева, Владимир Божилов
ATTENUATION EFFECT IN ALIPHATIC ACIDS EXTENDED TO ALKANES THE CARBON ACIDS VIA THE ALIPHATIC ALCOHOLS: AN EDUCATIONAL PERSPECTIVE IN CHEMISTRY
R. Sanjeev, V. Jagannadham
JACOB’S LADDER FOR THE PHYSICS CLASSROOM
Kristijan Shishkoski, Vera Zoroska
ЕХО ОТ МИНАЛОТО: АКТИВНОТО УЧИЛИЩЕ
Б. В. Тошев
COMPARATIVE PERFORMANCE AND DIGESTIBILITY OF NUTRIENTS IN AFSHARI AND GHEZEL RAM LAMBS
Morteza Karami
КАЛЦИЙ, ФОСФОР И ДРУГИ ФАКТОРИ ЗА КОСТНО ЗДРАВЕ
Радка Томова, Светла Асенова, Павлина Косева
Книжка 3
CONTENT AND LANGUAGE INTEGRATED LEARNING APPLIED TO TEACHING CHEMISTRY: A CASE STUDY FROM EASTERN EUROPE
Lino Bianco, Irina Andonova
IS ARGUMENTATIVE DRIVEN INQUIRY (ADI) THE FUTURE OF SCIENCE CLASSROOM?
James E. Hollenbeck, Michell Evans
ПРИРОДНИТЕ НАУКИ В PISA 2015: ДАННИ И ИЗВОДИ ОТ ВЪПРОСНИЦИТЕ
Адриана Тафрова-Григорова
SCIENCE FICTION TO PROMOTE SCIENCE: LEARNING LITERACY AND SOCIAL UNDERSTANDING
James E. Hollenbeck
ПРОУЧВАНЕ НА СПОСОБНОСТТА ЗА ОПЕРИРАНЕ С ОБРАЗИ НА ПРОСТРАНСТВОТО НА ОБИТАВАНАТА СРЕДА (МЕНТАЛНА КАРТА) НА СТУДЕНТИ ОТ ПЕДАГОГИЧЕСКИ СПЕЦИАЛНОСТИ
Мариан Георгиев Делчев
MATHEMATICAL MODELING OF 2019 NOVEL CORONAVIRUS (2019 – NCOV) PANDEMIC IN NIGERIA
Sefiu A. Onitilo, Mustapha A. Usman, Olutunde S. Odetunde, Fatai A. Hammed, Zacheous O. Ogunwobi, Hammed A. Haruna, Deborah O. Daniel
Книжка 2
ДОЦ. Д-Р СВОБОДА БЕНЕВА НА 80 ГОДИНИ
Мария Добрева
НАГРАДИТЕ НА ФОНДАЦИЯ „ВИГОРИЯ“ ЗА 2020 ГОДИНА
Мария Добрева
SODIUM-POTASSIUM PUMP AND BIOELECTROGENESIS IN TEACHING PHYSIOLOGY: MISCONCEPTIONS AND NEW DIDACTIC APPROACH
Petar Raychev
PHARMACOKINETICS, DRUG-LIKENESS, MEDICINAL PROPERTIES, MOLECULAR DOCKING ANALYSIS OF SUBSTITUTED Β-LACTAMS SYNTHEZIED VIA [BMIM][PF6]/]ET3NH]+[HSO4]CATALYZED COUPLING REACTION
Ajay M. Ghatole, Mahesh K. Gaidhane, Kushal R. Lanjewar, Kishor M. Hatzade
ИВАН Н. СТРАНСКИ – МИТЪТ И ЧОВЕКЪТ
Боян Мутафчиев
ВОДОРОДЪТ – НАЙ-ЕКОЛОГИЧНО ЧИСТОТО ГОРИВО
Miglena Slavova
Книжка 1
ФИЗИКАТА – НАВСЯКЪДЕ ОКОЛО НАС
Пенка Василева
ИЗВЪНКЛАСНИТЕ ДЕЙНОСТИ В УЧИЛИЩЕ
Петя Николаева
WATER PURIFICATION WITH LASER RADIATION
Lyubomir Lazov, Hristina Deneva, Galina Gencheva
НАБЛЮДЕНИЕ НА МЕТЕОРНИ ПОТОЦИ
Силвия Петрова
ОБЩА ОЦЕНКА НА ЕФЕКТИВНОСТТА НА ДЕЙНОСТИТЕ ЗА ПОСТИГАНЕ НА ОПТИМАЛНА СРЕДА ЗА ОБУЧЕНИЕ, НАУЧНИ ИЗСЛЕДВАНИЯ, ИНОВАЦИИ И УСТОЙЧИВО РАЗВИТИЕ НА ЧОВЕШКИЯ КАПИТАЛ В СФЕРАТА НА ХИМИЧЕСКИТЕ НАУКИ
Ивайла Панчева, Мирослава Недялкова, Петко Петков, Християн Александров, Васил Симеонов
ЕДИН УРОК ПО ФИЗИКА И АСТРОНОМИЯ В Х КЛАС: ВЪЛНИ НА ДЬО БРОЙЛ
Димитър Мърваков, Михаил Аврамов
ПЪРВИ СТЪПКИ В КВАНТОВАТА ФИЗИКА: ЕЛЕМЕНТАРНО ИЗЛОЖЕНИЕ – I МЕТОД
Михаил Аврамов, Димитър Мърваков
ФИЗИКОХИМИЧНАТА ШКОЛА НА РОСТИСЛАВ КАИШЕВ В ПЕРИОДА 1950 – 1957 (СПОМЕНИ НА ЕДИН СВИДЕТЕЛ)
Боян Мутафчиев
ПРОУЧВАНЕ НА НАГЛАСИТЕ НА БЪЛГАРСКИ УЧИТЕЛИ ПО ПРИРОДНИ НАУКИ ЗА ПРИЛОЖЕНИЕ НА КОМПЮТЪРНИ ТЕХНОЛОГИИ В КЛАС
Милена Кирова, Нели Киркова-Костова
2019 година
Книжка 6
48. НАЦИОНАЛНА КОНФЕРЕНЦИЯ НА УЧИТЕЛИТЕ ПО ХИМИЯ
Елена Бояджиева
ДИГИТАЛИЗАЦИЯ НА ОБРАЗОВАНИЕТО – НЕОБХОДИМОСТ И ПРОБЛЕМИ
Здравка Костова
LASER MICRO-PERFORATION AND FIELDS OF APPLICATION
Hristina Deneva, Lyubomir Lazov, Edmunds Teirumnieks
ELABORATION OF A LAB EXERCISE TO ANALYZE THE CHARACTERISTICS OF PHOTOVOLTAIC PANELS THROUGH A V-I ELECTRONIC UNIT
D. K. Gospodinov, D. A. Zlatanski, S. I. Sotirov
ПОЛИЕЛЕКТРОЛИТНИ КОМПЛЕКСИ МЕЖДУ ХИТОЗАН И АЛГИНАТ, ПОЛУЧЕНИ ЧРЕЗ СМЕСВАНЕ ПРИ ИНЖЕКТОРНО РАЗПРЪСКВАНЕ
Мария Марудова, Сотир Сотиров, Бисера Пиличева
ПРОЦЕСЪТ ДИФУЗИЯ – ОСНОВА НА ДИАЛИЗАТА
Берна Сабит, Джемиле Дервиш, Мая Никова, Йорданка Енева
IN VITRO EVALUATION OF THE ANTIOXIDANT PROPERTIES OF OLIVE LEAF EXTRACTS – CAPSULES VERSUS POWDER
Hugo Saint-James, Gergana Bekova, Zhanina Guberkova, Nadya Hristova-Avakumova, Liliya Atanasova, Svobodan Alexandrov, Trayko Traykov, Vera Hadjimitova
МОДЕЛ ЗА СЪДЪРЖАТЕЛНА И ТЕХНОЛОГИЧНА ИНТЕГРАЦИЯ В ЕКОЛОГИЧНОТО ОБРАЗОВАНИЕ
Клаида Дойчинова, Надежда Райчева
Бележки върху нормативното осигуряване на оценяването в процеса
БЕЛЕЖКИ ВЪРХУ НОРМАТИВНОТО ОСИГУРЯВАНЕ, НА ОЦЕНЯВАНЕТО В ПРОЦЕСА НА ОБУЧЕНИЕТО
АНАЛИЗ НА РЕЗУЛТАТИТЕ ОТ ВЪНШНИТЕ ОЦЕНЯВАНИЯ ПО ГЕОГРАФИЯ И ИКОНОМИКА В V КЛАС, ПРОВЕДЕНИ ПРЕЗ 2017 И 2018 Г.
Иван Дреновски, Илияна Русева
ПАРАЦЕЛЗ В ИСТОРИЯТА НА ХИМИЯТА, МЕДИЦИНАТА И ФАРМАЦИЯТА
Нано Рангелов Степанов
ТЕХНОЛОГИЯ
Б. В. Тошев
Книжка 5
PROSPECTIVE SCIENCE TEACHERS UNDERSTANDING OF KINEMATIC GRAPHS IN COLLABORATIVE SOCRATIC QUESTIONING COURSE ACCOMPANIED BY WEB-BASED FORMATIVE ASSESSMENT
Intan E. Kirana, Sentot Kusairi, Arif Hidayat
VISUALIZATION AS A COMPONENT OF THE EDUCATIONAL PROCESS IN THE COURSE OF ANALYTICAL CHEMISTRY FOR STUDENTS OF TECHNOLOGICAL SPECIALTIES
Т. Kudyrko, Е. Tomashova
ПРОФ. Д.Н. ЕЛЕНА КИРКОВА НАВЪРШИ 96 ГОДИНИ: ИНТЕРВЮ
Адриана Тафрова-Григорова
ЕМИЛ ФИШЕР (1852 – 1919) – МАГЪТ НА ХИМИЧЕСКИЯ СИНТЕЗ
Нано Степанов
ON THE GENETIC TIES BETWEEN EUROPEAN NATIONS
Jordan Tabov, Nevena Sabeva-Koleva, Georgi Gachev
SCIENCE CAN BRING PEOPLE TOGETHER An Interview with Fabiola Gianotti, Director-General, CERN
Nadya Kantareva-Baruh
ACHIEVING EFFECTIVE TEACHING OF MODULE “CHEMICAL KINETICS – CHEMICAL EQUILIBRIUM” WITH THE AID OF AN INTEGRATED WEBSITE
A. Thysiadou, I. Sakla, P. Giannakoudakis
Иван Странски – майсторът на кристалния растеж [Ivan Stranski
ИВАН СТРАНСКИ – МАЙСТОРЪТ, НА КРИСТАЛНИЯ РАСТЕЖ
CHEMISTRY EDUCATION: CURRENT BIBLIOGRAPHY (2018)
B. V. Toshev
Детето и учебните програми [The Child and Curricula] / Д. Дюи /
ДЕТЕТО И УЧЕБНИТЕ ПРОГРАМИ
Книжка 4
CHEMOMETRIC ANALYSIS OF SCHOOL LIFE IN VARNA
Radka Tomova, Petinka Galcheva, Ivajlo Trajkov, Antoaneta Hineva, Stela Grigorova, Rumyana Slavova, Miglena Slavova
НАГЛАСИ НА 13 – 14-ГОДИШНИ УЧЕНИЦИ КЪМ ПРИРОДНИТЕ НАУКИ В НЕФОРМАЛНА ОБРАЗОВАТЕЛНА СРЕДА
Явор Киряков, Иса Хаджиали, Димитър Грозев
AN ANALYTICAL EXPERIMENT USING BEER’S LAW FOR A MIXTURE OF TWO DYES
A.E. Burns, N.G. Burns, C. Kramer
SYNTHESIS OF POLY(TETRAHYDROFURAN- CO-EPICHLOROHYDRIN) USING AN ECOLOGIC CATALYST MONTMORILLONITE (MAGHNITE-H+)
Hamam Nabil, Sari Fouad, Ferrahi Mohammed Issam, Belbachir Mohammed
CONSTRUCTION OF JOB’S PLOT IN CASE OF HIGH SPECTRAL OVERLAP BETWEEN THE REACTANTS AND THE COMPLEX: APPLICATION OF MULTIWAVELENGTH LINEAR REGRESSION ANALYSIS USING THE CU-EDTA SYSTEM
Agha Arslan Wasim, Muhammad Nasiruddin Khan, Muhammad Farooq Wahab, Saba Fazal-ur-Rehman
SPECTRAL, BIOLOGICAL, MAGNETIC AND CONDUCTANCE STUDIES ON THE COORDINATION COMPOUNDS OF A NEWLY SYNTHESIZED THIAZOLIDIN-4-ONE
Dinesh Kumar, Amit Kumar
ЦИКЛИТЕ НА КРЕБС
Ивелин Кулев
Книжка 3
ПРИНЦИПИТЕ НА КАРИЕРНОТО РАЗВИТИЕ НА МЛАДИЯ УЧЕН
И. Панчева, М. Недялкова, С. Кирилова, П. Петков, В. Симеонов
УЧЕНИЧЕСКИ ПОГРЕШНИ СХВАЩАНИЯ, СВЪРЗАНИ С ХИМИЧНОТО РАВНОВЕСИЕ
Кирил Атанасов, Александрия Генджова
UTILISATION OF THE STATIC EVANS METHOD TO MEASURE MAGNETIC SUSCEPTIBILITIES OF TRANSITION METAL ACETYLACETONATE COMPLEXES AS PART OF AN UNDERGRADUATE INORGANIC LABORATORY CLASS
Anton Dobzhenetskiy, Callum A. Gater, Alexander T. M. Wilcock, Stuart K. Langley, Rachel M. Brignall, David C. Williamson, Ryan E. Mewis
STUDY OF MOROCCAN PUPILS’ SKILLS IN SOLVING CHEMISTRY PROBLEMS AT FIRST YEAR OF HIGH-SCHOOL
Ali Ouasri
ESTIMATION OF GENOTOXIC EFFECT OF INSECTICIDE CHROMAGOR AT GOLDFISH (CARASSIUS AURATUS) AFTER 5 DAYS OF TREATMENT
Kemajl Kurteshi, Zeqir Shaqiri
BIOACCUMULATION OF CADMIUM IN EDIBLE WILD MUSHROOM (SUILLUS LUTEUS), BULGARIA
P. Papazov, P. Denev
THE 100
Maria Atanassova, Radoslav Angelov
A TALE OF SEVEN SCIENTISTS
Scerri, E.R. (2016). A Tale of Seven Scientists and a New Philosophy of Science.
Книжка 2
DEVELOPMENT OF A LESSON PLAN ON THE TEACHING OF MODULE “WATER CONDUCTIVITY”
A. Thysiadou, S. Christoforidis, P. Giannakoudakis
CHEMISTRY STUDENTS’ DIFFICULTIES IN LEARNING OXIDATION-REDUCTION REACTIONS
Kenneth Adu-Gyamfi, Joseph Ghartey Ampiah
ИЗСЛЕДВАНЕ ВИЗИЯТА НА СТУДЕНТИ ПЕДАГОЗИ ОТНОСНО РОЛЯТА НА ИЗУЧАВАНЕТО НА СЕЗОННИТЕ ИЗМЕНЕНИЯ ЗА ИЗГРАЖДАНЕ ОСНОВИТЕ НА ПРИРОДОНАУЧНОТО ОБРАЗОВАНИЕ В I – IV КЛАС
Ваня Петрова, Мариан Делчев
ФОРМИРАНЕ НА КЛЮЧОВИ КОМПЕТЕНТНОСТИ В ЧАСОВЕТЕ ПО „БИОЛОГИЯ И ЗДРАВНО ОБРАЗОВАНИЕ“, IX КЛАС, ЧРЕЗ ИЗПОЛЗВАНЕ НА ИНТЕРАКТИВНИ МЕТОДИ
Росица Давидова, Красимира Томева, Мария Бойчева
AMPEROMETRIC NITRIC OXIDE SENSOR BASED ON MWCNT CHROMIUM(III) OXIDE NANOCOMPOSITE
Arsim Maloku, Epir Qeriqi, Liridon S. Berisha, Ilir Mazreku, Tahir Arbneshi, Kurt Kalcher
THE EFFECT OF AGING TIME ON Mg/Al HYDROTALCITES STRUCTURES
Eddy Heraldy, Triyono, Sri Juari Santosa, Karna Wijaya, Shogo Shimazu
Книжка 1
A CONTENT ANALYSIS OF THE RESULTS FROM THE STATE MATRICULATION EXAMINATION IN MATHEMATICS
Elena Karashtranova, Nikolay Karashtranov, Vladimir Vladimirov
ВАРИАНТИ НА ОБУЧЕНИЕ, БАЗИРАНИ НА КОНСТРУКТИВИЗМА
Юрий Клисаров
SOME CONCEPTS FROM PROBABILITY AND STATISTICS AND OPPORTUNITIES TO INTEGRATE THEM IN TEACHING NATURAL SCIENCES
Elena Karashtranova, Nikolay Karashtranov, Nadezhda Borisova, Dafina Kostadinova
REVIEW AND IMPROVED TECHNIQUE OF THE INITIAL RATE METHOD
Patiha, Maulidan Firdaus
45. МЕЖДУНАРОДНА ОЛИМПИАДА ПО ХИМИЯ
Донка Ташева, Пенка Василева
SEMI-EMPIRICAL COMPUTATIONAL STUDY OF THE LIGAND AND ITS METAL COMPLEXES DERIVED FROM 4- AMINOANTIPYRINE AND 2, 4-DIHYDROXY BENZOIC ACID
Satya Narayan Chaulia
ADVANCES OF PHOTOTHERMAL MICROSCOPY OF COMPOSITE MAGNETOELECTRIC NANOLAYERS USING LASER HETERODYNE PROBE
Vasilka Pencheva, Stoyan Penchev, Lyuben Ivanov
2018 година
Книжка 6
ЗДРАВЕ И ОКОЛНА СРЕДА
Кадрие Шукри, Светлана Великова, Едис Мехмед
В ТЪРСЕНЕ НА ТАЛАНТЛИВИ И НАДАРЕНИ УЧЕНИЦИ
Жана Кюркчиева
ПРОФЕСИОНАЛНАТА УЧЕБНА ОБЩНОСТ
Станимира Савова
ФИЗИКАТА, ЧОВЕКЪТ И ПРИРОДАТА И ДЕЦАТА НА НОВОТО ВРЕМЕ
Роза Рангелова, Милена Маврова
ОПРЕДЕЛЯНЕ НА ЗЕМНОТО УСКОРЕНИЕ: ЕКСПЕРИМЕНТАЛНА ЗАДАЧА
Мариана Анастасова
МОДЕЛ ЗА ИЗУЧАВАНЕ НА МЕХАНИЧНИ ТРЕПТЕНИЯ И ВЪЛНИ В СРЕДНОТО УЧИЛИЩЕ (IX КЛАС) С ПРИЛАГАНЕ НА ИЗСЛЕДОВАТЕЛСКИ ПОДХОД
Костадина Кацарова, Желязка Райкова
РОБОТИКА ЗА НАЧИНАЕЩИ ЕНТУСИАСТИ
Даниела Узунова, Борис Велковски, Илко Симеонов, Владислав Шабански, Димитър Колев
ДИСЦИПЛИНАТА „ПРОИЗХОД НА ЖИВОТА И ТЕОРИИ ЗА ЕВОЛЮЦИЯТА“ В ПРОФЕСИОНАЛНАТА ПОДГОТОВКА НА УЧИТЕЛЯ ПО БИОЛОГИЯ
Иса Хаджиали
DESIGN AND DOCKING STUDIES OF HIS-LEU ANALOGUES AS POTENTIOAL ACE INHIBITORS
Rumen Georgiev, , Tatyana Dzimbova, Atanas Chapkanov
X-RAY DIFFRACTION STUDY OF M 2 Zn(TeО3)2 (M - Na, K) ТELLURIDE
Kenzhebek T. Rustembekov, Mitko Stoev, Aitolkyn A. Toibek
CALIBRATION OF GC/MS METHOD FOR DETERMINATION OF PHTHALATES
N. Dineva, I. Givechev, D. Tanev, D. Danalev
ELECTROSYNTHESIS OF CADMIUM SELENIDE NANOPARTICLES WITH SIMULTANEOUS EXTRACTION INTO P-XYLENE
S. S. Fomanyuk, V. O. Smilyk, G. Y. Kolbasov, I. A. Rusetskyi, T. A. Mirnaya
SYNTHESIS AND CHARACTERIZATION OF NOVEL HETEROCYCLES WITH ANTICIPATED ANTIMICROBIAL ACTIVITIES FROM PYRANOPYRAZOLE DERIVATIVE
H.M.F. Madkour, O.E.A. Mostafa, E.A. El-Bordany, A.K. El-Ziaty, M. Nabil
БИОЛОГИЧЕН АСПЕКТ НА РЕКАНАЛИЗАЦИЯ С ВЕНОЗНА ТРОМБОЛИЗА
Мариела Филипова, Даниела Попова, Стоян Везенков
CHEMISTRY: BULGARIAN JOURNAL OF SCIENCE EDUCATION ПРИРОДНИТЕ НАУКИ В ОБРАЗОВАНИЕТО VOLUME 27 / ГОДИНА XXVII, 2018 ГОДИШНО СЪДЪРЖАНИЕ СТРАНИЦИ / PAGES КНИЖКА 1 / NUMBER 1: 1 – 152 КНИЖКА 2 / NUMBER 2: 153 – 312 КНИЖКА 3 / NUMBER 3: 313 – 472 КНИЖКА 4 / NUMBER 4: 473 – 632 КНИЖКА 5 / NUMBER 5: 633 – 792 КНИЖКА 6 / NUMBER 6: 793 – 952 КНИЖКА 1 / NUMBER 1: 1 – 152 КНИЖКА 2 / NUMBER 2: 153 – 312 КНИЖКА
(South Africa), A. Ali, M. Bashir (Pakistan) 266 – 278: j-j Coupled Atomic Terms for Nonequivalent Electrons of (n-1)fx and nd1 Configurations and Correlation with L-S Terms / P. L. Meena (India) 760 – 770: Methyl, тhe Smallest Alkyl Group with Stunning Effects / S. Moulay 771 – 776: The Fourth State of Matter / R. Tsekov
Книжка 5
ИМОБИЛИЗИРАНЕНАФРУКТОЗИЛТРАНСФЕРАЗА ВЪРХУКОМПОЗИТНИФИЛМИОТПОЛИМЛЕЧНА КИСЕЛИНА, КСАНТАН И ХИТОЗАН
Илия Илиев, Тонка Василева, Веселин Биволарски, Ася Виранева, Иван Бодуров, Мария Марудова, Теменужка Йовчева
ELECTRICAL IMPEDANCE SPECTROSCOPY OF GRAPHENE-E7 LIQUID-CRYSTAL NANOCOMPOSITE
Todor Vlakhov, Yordan Marinov, Georgi. Hadjichristov, Alexander Petrov
SURFACE PHOTOVOLTAGE SPECTROSCOPY CHARACTERIZATION OF GAASSBN LAYERS GROWN BY LIQUID-PHASE EPITAXY
S. Georgiev, V. Donchev, M. Milanova
ON THE POSSIBILITY TO ANALYZE AMBIENT NOISERECORDED BYAMOBILEDEVICETHROUGH THE H/V SPECTRAL RATIO TECHNIQUE
Dragomir Gospodinov, Delko Zlatanski, Boyko Ranguelov, Alexander Kandilarov
RHEOLOGICAL PROPERTIES OF BATTER FOR GLUTEN FREE BREAD
G. Zsivanovits, D. Iserliyska, M. Momchilova, M. Marudova
THE EFFECT OF HYDROCOLLOIDS CONCENTRATION ON THE PHYSICAL PROPERTIES OF GLUTEN-FREE CAKE
Dida Iserliyska, Gabor Zsivanovits, Maria Marudova
ПОЛУЧАВАНЕ НА ПОЛИЕЛЕКТРОЛИТНИ КОМПЛЕКСИ ОТ ХИТОЗАН И КАЗЕИН
Антоанета Маринова, Теменужка Йовчева, Ася Виранева, Иван Бодуров, Мария Марудова
DISTRIBUTION OF LAMB WAVES IN AlScN RESONATOR STRUCTURES
Boris Nedyalkov, Evgenia Valcheva
CHEMILUMINESCENT AND PHOTOMETRIC DETERMINATION OF THE ANTIOXIDANT ACTIVITY OF COCOON EXTRACTS
Y. Evtimova, V. Mihailova, L. A. Atanasova, N. G. Hristova-Avakumova, M. V. Panayotov, V. A. Hadjimitova
ИНТЕРДИСЦИПЛИНАРНИТЕ УРОЦИ – ПРЕДИЗВИКАТЕЛСТВО ЗА УЧЕНИЦИТЕ И УЧИТЕЛИТЕ ПО ПРИРОДНИ НАУКИ
Юлиана Белчева, Радостина Захариева
ИЗСЛЕДОВАТЕЛСКИ ПРАКТИКУМ
Ивелина Димитрова, Гошо Гоев, Савина Георгиева, Цвета Цанова, Любомира Иванова, Борислав Георгиев
ИСТОРИЧЕСКОТО РАЗВИТИЕ НА ИДЕИТЕ ЗА ХИМИЧНА ОБРАТИМОСТ И ХИМИЧНО РАВНОВЕСИЕ – ОСНОВА ЗА ПРЕПОДАВАНЕТО И ИЗУЧАВАНЕТО ИМ
К. Атанасов, А. Генджова
ИНСТРУМЕНТИ ЗА ИЗПОЛЗВАНЕ НА ХИМИЧЕН ЕКСПЕРИМЕНТ И САМООЦЕНКА В СТРАТЕГИИТЕ ЗА АКТИВНО ОБУЧЕНИЕ ПО „ЧОВЕКЪТ И ПРИРОДАТА“ 1)
Калина Иванова
НОВИ ИЗМЕРЕНИЯ НА УЧЕНЕТО: СИНТЕЗ НА ИНОВАЦИИ И ТРАДИЦИИ
Любомир С. Георгиев
Книжка 4
МИЛКА ДЖИДЖОВА: С ОТГОВОРНОСТ И ВСЕОТДАЙНОСТ КЪМ МЛАДИТЕ
Мария Добрева
НАШИЯТ ОПИТ В ОБУЧЕНИЕТО ПО АСТРОНОМИЯ
Свежина Димитрова
PARAMETRIC INTERACTION OF OPTICAL PULSES IN NONLINEAR ISOTROPIC MEDIUM
A. Dakova, V. Slavchev, D. Dakova, L. Kovachev
ИЗСЛЕДВАНЕ НА ПОЛИМЕРНИ МАТЕРИАЛИ С ПОМОЩТА НА ЕЛЕКТРОАКУСТИЧЕН И ВИХРОВОЛТОВ МЕТОД
Радостин Касъров, Самуил Динев
UNIFYING THE ANALYTICAL SOLUTIONS OF THE GEODESIC EQUATIONS IN BONDI-GOLD-HOYLЕ UNIVERSE MODEL
Plamena I. Marcheva, Diana Y. Dakova, Stoil I. Ivanov
ДЕЙСТВИЕ НА ГАМА-ЛЪЧИТЕ ВЪРХУ ДЕЗОКСИРИБОНУКЛЕИНОВАТА КИСЕЛИНА
Мирела Вачева, Хари Стефанов, Йоана Гвоздейкова, Йорданка Енева
RADIATION PROTECTION
Natasha Ivanova, Bistra Manusheva
СТАБИЛНОСТ НА ЕМУЛСИИ ОТ ТИПА МАСЛО/ ВОДА С КОНЮГИРАНА ЛИНОЛОВА КИСЕЛИНА
И. Милкова-Томова, Д. Бухалова, К. Николова, Й. Алексиева, И. Минчев, Г. Рунтолев
THE EFFECT OF EXTRA VIRGIN OLIVE OIL ON THE HUMAN BODY AND QUALITY CONTROL BY USING OPTICAL METHODS
Carsten Tottmann, Valentin Hedderich, Poli Radusheva, Krastena Nikolova
ИНФРАЧЕРВЕНА ТЕРМОГРАФИЯ ЗА ДИАГНОСТИКА НА ФОКАЛНА ИНФЕКЦИЯ
Рая Грозданова-Узунова, Тодор Узунов, Пепа Узунова
ЕЛЕКТРИЧНИ СВОЙСТВА НА КОМПОЗИТНИ ФИЛМИ ОТ ПОЛИМЛЕЧНА КИСЕЛИНА
Ася Виранева, Иван Бодуров, Теменужка Йовчева
NINE HYPOTHETICAL PROBLEMS FOR LINKAGE BETWEEN QUALITATIVE ANALYSIS AND STOICHIOMETRIC CALCULATIONS
Soner Ergül
MATHEMATICAL MODELING AND EFFECT OF ISOTHERMAL DRYING ON MUSHROOM (BOLETUS PINOPHILUS)
M. Ivanova, P. Papazov, L. Dospatliev, N. Katrandzhiev
Книжка 3
Physics is an Ever Young Science [Физиката – вечно млада наука] / T. Yovcheva /
Temenuzhka Yovcheva
EMPIRICAL BAYESIAN ESTIMATES OF OPERATIONAL RELIABILITY RELATED TO ELECTRONIC ITEMS FOR MEDICAL PURPOSE
Julia Garipova, Penka Georgieva, Anton Georgiev
МЕЖДУНАРОДНА АСТРОНОМИЧЕСКА ПРОГРАМА ЗА ТЪРСЕНЕ НА АСТЕРОИДИ – СЪТРУДНИЧЕСТВО МЕЖДУ УЧЕНИ, СТУДЕНТИ И УЧЕНИЦИ
Веселка Радева
ТРИ ИДЕИ ЗА ЕФЕКТИВНО ОБУЧЕНИЕ
Гергана Карафезиева
ОПТИЧНИ ЯВЛЕНИЯ В ПРИРОДАТА
Теодора Ганчева
МАГИЯТА НА ТВОРЧЕСТВОТО КАТО ПЪТ НА ЕСТЕСТВЕНО УЧЕНЕ В УЧЕБНИЯ ПРОЦЕС
Гергана Добрева, Жаклин Жекова, Михаела Чонос
ИЗВЪНКЛАСНИ ФОРМИ НА РАБОТА ПО АСТРОНОМИЯ
Радка Костадинова
ОБУЧЕНИЕ ПО ПРИРОДНИ НАУКИ ЧРЕЗ МИСЛОВНИ КАРТИ
Виолета Стоянова, Павлина Георгиева
ИНТЕРАКТИВНИТЕ МЕТОДИ И ЕКОЛОГИЧНОТО ОБРАЗОВАНИЕ НА УЧЕНИЦИТЕ В ОБУЧЕНИЕТО ПО „ЧОВЕКЪТ И ПРИРОДАТА“ В V И VI КЛАС
Нели Димитрова, Даниела Димова
ИГРА НА ДОМИНО В ЧАС ПО ФИЗИКА
Росица Кичукова, Ценка Маринова
ВИЗУАЛИЗАЦИИ В ОБУЧЕНИЕТО ПО ФИЗИКА И АСТРОНОМИЯ
Антоанета Димитрова
ПРОБЛЕМИ ПРИ ОБУЧЕНИЕТО ПО ФИЗИКА ВЪВ ВВМУ „Н. Й. ВАПЦАРОВ“
А. Христова, Г. Вангелов, И. Ташев, М. Димидов
ИЗГРАЖДАНЕ НА СИСТЕМА ОТ УЧЕБНИ ИНТЕРНЕТ РЕСУРСИ ПО ФИЗИКА И ОЦЕНКА НА ДИДАКТИЧЕСКАТА ИМ СТОЙНОСТ
Желязка Райкова, Георги Вулджев, Наталия Монева, Нели Комсалова, Айше Наби
ПРОВЕЖДАНЕ НА СЪСТЕЗАНИЕ ПО ПРИЛОЖНА ЕЛЕКТРОНИКА В НАЦИОНАЛНИЯ ВОЕНЕН УНИВЕРСИТЕТ „ВАСИЛ ЛЕВСКИ“ И НЕГОВОТО РАЗВИТИЕ И ВЛИЯНИЕ ВЪРХУ ОБУЧАЕМИТЕ
Николай Долчинков
ПРОВЕЖДАНЕНАФОТОКОНКУРСИИ КОНКУРСИ ЗА ПОСТЕРИ В НАЦИОНАЛНИЯ ВОЕНЕН УНИВЕРСИТЕТ „ВАСИЛ ЛЕВСКИ“ И ДОБРАТА СЪВМЕСТНА РАБОТА С ДРУГИ УНИВЕРСИТЕТИ И ШИРОК КРЪГ УЧИЛИЩА
Николай Долчинков
ИНОВАЦИИ В БОРБАТА С ТУМОРНИ ОБРАЗУВАНИЯ – ЛЕЧЕНИЕ ЧРЕЗ БРАХИТЕРАПИЯ
Георги Върбанов, Радостин Михайлов, Деница Симеонова, Йорданка Енева
INFLUENCE OF THE GINGIVAL TISSUES ON THE MEASURED SATURATION LEVEL OF THE DENTAL PULP BLOOD FLOW
Dimitar Kosturkov, Tsonko Uzunov, Pepa Uzunova
NATURAL RADIONUCLIDES IN DRINKING WATER
Natasha Ivanova, Bistra Manusheva
Книжка 2
РАЗВИВАНЕ НА ТВОРЧЕСКИТЕ СПОСОБНОСТИ НА УЧЕНИЦИТЕ В ОБУЧЕНИЕТО ПО „ХИМИЯ И ОПАЗВАНЕ НА ОКОЛНАТА СРЕДА ЧРЕЗ МЕТОДА НА ПРОЕКТИТЕ 1)
Душка Ростиславова Станковска
ОБУЧЕНИЕТО ПО ПРИРОДНИ НАУКИ В V – VII КЛАС И НЯКОИ ВЪЗМОЖНОСТИ ЗА ФОРМИРАНЕ НА ПРИРОДОНАУЧНА ГРАМОТНОСТ У УЧЕНИЦИТЕ1)
Величка Димитрова, Силвия Попова
ВЪЗГЛЕДИ НА БЪЛГАРСКИ ГИМНАЗИСТИ ЗА СЪЩНОСТТА НА НАУКАТА И НАУЧНОТО ИЗСЛЕДВАНЕ – ДЖЕНДЪРЕН АСПЕКТ
Иса Хаджиали, Йорданка Димова, Златка Гарова
АДАПТИРАНЕ НА ОБРАЗОВАНИЕТО ДНЕС ЗА УТРЕШНИЯ ДЕН
И. Панчева, М. Недялкова, П. Петков, Х. Александров, В. Симеонов
INVESTIGATING VIEWS OF STEM PRIMARY TEACHERS ON STEM EDUCATION
Prasart Nuangchalerm
TEACHING ELECTRICITY WITH A ROLE PLAY
Mehmet Karakas
STRUCTURAL ELUCIDATION OF UNKNOWNS: A SPECTROSCOPIC INVESTIGATION WITH AN EMPHASIS ON 1D AND 2D 1H NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY
Vittorio Caprio, Andrew S. McLachlan, Oliver B. Sutcliffe, David C. Williamson, Ryan E. Mewis
SYNTHESIS AND CHARACTERIZATION OF ALUMINIUM 2024 WITH TUNGSTEN CARBIDE METAL MATRIX COMPOSITE BY IN-SITU METHOD
S. Nallusamy, M. Rajaram Narayanan, S. Saravanan
DETERMINATION OF VITAMINS B AND C IN THE BIOMASS GROWN ON THE OLIVE MILL WASTEWATER IN SYRIA BY HPCL METHOD
Mariam Darakli, Ahmad Malo, Adnan Shhadeh
ALEKSANDЕR HERD’S TEACHING LEGACY IN THE CONTEXT OF THE DEVELOPMENT OF MODERN NATURAL SCIENCES EDUCATION
M. M. Holovkova, A. A. Korobchenko, Y. I. Popeleshko
j-j Coupled Atomic Terms for Nonequivalent Electrons of (n-1)f
j-jCOUPLEDATOMICTERMSFORNONEQUIVALENT, ELECTRONS OF (n-f X nd CONFIGURATIONS AND, CORRELATION WITH L-S TERMS
ОНЛАЙН ЕЛЕКТРОНЕН ТЕСТ С ФОРМАТ НА МАТУРА ПО ГЕОГРАФИЯ, ПРОВЕЖДАН ОТ ЮГОЗАПАДНИЯ УНИВЕРСИТЕТ „НЕОФИТ РИЛСКИ“ – БЛАГОЕВГРАД
Иван Дреновски
INTEGRATED ENGINEERING EDUCATION: THE ROLE OF ANALYSIS OF STUDENTS’ NEEDS
Veselina Kolarski, Dancho Danalev, Senia Terzieva
УЧЕНЕТО В ПРИРОДОНАУЧНОТО ПОЗНАНИЕ И СТРАХЪТ ОТ ПРОВАЛ
Николай Цанков, Веска Гювийска
КНИГА ЗА УЧИТЕЛЯ ПО ХИМИЯ: VIII КЛАС (2017)
Б. В. Тошев
Книжка 1
УСПЕШНИЯТ УЧИТЕЛ ПРЕЗ ПОГЛЕДА НА КОНСТРУКТИВИСТКИТЕ ИДЕИ
Владимир Цветков, Елена Бояджиева
ВЪЗГЛЕДИ НА БЪЛГАРСКИ ГИМНАЗИСТИ ЗА СЪЩНОСТТА НА НАУКАТА И НАУЧНОТО ИЗСЛЕДВАНЕ
Златка Гарова, Веска Нончева, Йорданка Димова
INTEGRATION OF SCIENCE, TECHNOLOGY, ENGINEERING AND MATHEMATICS: THE MULTIDISIPLINARY APPROACH TO ENHANCE THE ENVIRONMENTAL LITERACY OF PROSPECTIVE CHEMISTRY TEACHERS
Ratna Farwati, Anna Permanasari, Harry Firman, Tatang Suhery
РЕЗУЛТАТИ ОТ ОБУЧЕНИЕТО НА СТУДЕНТИ – БЪДЕЩИ УЧИТЕЛИ ПО БИОЛОГИЯ, С ЦЕЛ ФОРМИРАНЕ НА МЕТОДИЧЕСКИ УМЕНИЯ ЗА РАБОТА С ИНТЕРАКТИВНИ МЕТОДИ
Мария Бойчева, Росица Давидова, Анита Петрова
EXPERIMENTAL AND COMPUTATIONAL STUDY OF Co(II), Ni(II), Cu(II) AND Zn(II) COMPLEXES WITH THE AZO DYE DERIVED FROM 2-AMINO-4-METHYL PYRIDINE AND β-NAPTHOL
Satya Narayan Chaulia
ZAGREB CONNECTION INDICES OF TiO2 NANOTUBES
Sohaib Khalid, Johan Kok, Akbar Ali, Mohsin Bashir
EFFECT OF UNTREATED OLIVE MILL WASTEWATER ON SEED GERMINATION, SEEDLING GROWTH AND BIOCHEMICAL OF MAIZE (ZEA MAYS L.)
Manar Abu-Hassan, Ahmad Malo, Nadim Al-Muhanna
SYNTHESIS OF NEW 3-[(CHROMEN-3-YL)ETHYLIDENEAMINO]-PHENYL]-THIAZOLIDIN-4ONES AND THEIR ANTIBACTERIAL ACTIVITY
Ramiz Hoti, Naser Troni, Hamit Ismaili, Malesore Pllana, Musaj Pacarizi, Veprim Thaçi, Gjyle Mulliqi-Osmani
THE INFLUENCE OF CHANGES IN THE HYDROLOGICAL REGIME OF THE URAL RIVER IN THE WEST KAZAKHSTAN REGION ON FISH RESOURCES
Arkady Kim, Turesh Murzashev, Daniyar Tagayev, Zhaskhaiyr Karagoishin
2017 година
Книжка 6
THE TEACHING METHOD NAMED “STARTER-EXPERIMENT-APPROACH”
Naim Syla, Gezim Hodolli
EMPOWERING STUDENTS’ CHEMISTRY LEARNING: THE INTEGRATION OF ETHNOCHEMISTRY IN CULTURALLY RESPONSIVE TEACHING
Yuli Rahmawati, Achmad Ridwan
„БЪЛГАРСКИТЕ ИМЕНА В СЛЪНЧЕВАТА СИСТЕМА“ – ОБУЧЕНИЕ ПО АСТРОНОМИЯ С ПРИЛАГАНЕ НА ИНОВАЦИОННИ МЕТОДИ, ЕМОЦИОНАЛНО ВЪЗДЕЙСТВИЕ И АНГАЖИРАНОСТ
В. Радева, Д. Kюркчиева
РАЗВИВАНЕ НА ПРИРОДОНАУЧНА ГРАМОТНОСТ ЧРЕЗ ВЪВЕЖДАНЕ МОДЕЛ НА АКТИВНО ОБУЧЕНИЕ И УЧЕНЕ ЧРЕЗ СЪТРУДНИЧЕСТВО
Маргарита Бозова
АКАДЕМИК АЛЕКСЕЙ ШЕЛУДКО (1920 – 1995)
Димо Платиканов
GEOECOLOGICAL ANALYSIS OF INDUSTRIAL CITIES: ON THE EXAMPLE OF AKTOBE AGGLOMERATION
Zharas Berdenov, Erbolat Mendibaev, Talgat Salihov, Kazhmurat Akhmedenov, Gulshat Ataeva
TECHNOGENESIS OF GEOECOLOGICAL SYSTEMS OF NORTHEN KAZAKHSTAN: PROGRESS, DEVELOPMENT AND EVOLUTION
Kulchichan Dzhanaleyeva, Gulnur Mazhitova, Altyn Zhanguzhina, Zharas Berdenov, Tursynkul Bazarbayeva, Emin Atasoy
ANTIOXIDANT ACTIVITY, PHENOLS, FLAVONOIDS, FLAVONOLS AND ANTHOCYANINS CONTENT OF TUSSILAGO FARFARA (L.) GROWING WILD IN KOSOVO
Fatmir Faiku, Arben Haziri, Bleron Faiku
ПРОФ. Д.Х.Н. ДИМО ПЛАТИКАНОВ (1936 – 2017)
PROF. DIMO PLATIKANOV (1936 – 2017)
СПИСАНИЕ ПРОСВѢТА
Списание „Просвета“ е орган на Просветния съюз в България. Списанието е излизало всеки месец без юли и август. Годишният том съдържа 1280 стра- ници. Списанието се издава от комитет, а главен редактор от 1935 до 1943 г. е проф. Петър Мутафчиев, историк византолог и специалист по средновеков-
Книжка 5
47-А НАЦИОНАЛНА КОНФЕРЕНЦИЯ НА УЧИТЕЛИТЕ ПО ХИМИЯ
В последните години тези традиционни за българското учителство конфе- ренции се организират от Българското дружество по химическо образование и история и философия на химията. То е асоцииран член на Съюза на химици- те в България, който пък е член на Европейската асоциация на химическите и
JOURNALS OF INTEREST: A REVIEW (2016)
BULGARIAN JOURNAL OF SCIENCE AND EDUCATION POLICY ISSN 1313-1958 (print) ISSN 1313-9118 (online) http://bjsep.org
„НАВАКСВАНЕТО“ В VII КЛАС, ИЛИ ДИРИЖИРАНИЯТ ХАОС В „ПРИЛАГАНЕТО“ НА НОВИЯ ОБРАЗОВАТЕЛЕН ЗАКОН
Иван Дреновски, Илияна Русева
КАК БИ ТРЯБВАЛО ДА ИЗГЛЕЖДА НОВАТА УЧЕБНА ПРОГРАМА ПО ГЕОГРАФИЯ И ИКОНОМИКА ЗА VIII КЛАС?
Иван Дреновски, Илияна Русева
ON THE PLACEMENT OF HYDROGEN AND HELIUM IN THE PERIODIC SYSTEM: A RESPONSE TO CVETKOVIĆ & PETRUŠEVSKI
Martín Labarca, Akash Srivaths
HIGHER EDUCATION IN ENGINEERING AND TECHNOLOGY – THE PRESENT SCENARIO
T. G. Balachandran, S. Sendilvelan
ПРОЕКТИРАНЕ НА ОБРАЗОВАТЕЛНА ТЕХНОЛОГИЯ ПО „ИНЖЕНЕРНА ЕКОЛОГИЯ“
Надя Илиева, Елена Бояджиева
INVESTIGATING THE ABILITY OF 8
Marina Stojanovska, Vladimir M. Petruševski
CONTEXT-BASED STUDENT RESEARCH PROJECT WORK WITHIN THE FRAMEWORK OF THE ANALYTICAL CHEMISTRY COURSE
N. Stozhko, B. Bortnik, A. Tchernysheva, E. Podshivalova
SYNTHESIS OF TiO -M (Cd, Co, Mn)
Candra Purnawan, Sayekti Wahyuningsih, Dwita Nur Aisyah
A NOVEL APPROACH FOR KINETIC STUDY OF ALKALINE HYDROLYSIS OF ETHYL ACETATE
Mala Das Sharma, U.S.V.R. Hymavathi
EFFECT OF DIFFERENT CADMIUM CONCENTRATION ON SOME BIOCHEMICAL PARAMETERS IN ‘ISA BROWN’ HYBRID CHICKEN
Imer Haziri, Adem Rama, Fatgzim Latifi, Dorjana Beqiraj-Kalamishi, Ibrahim Mehmeti, Arben Haziri
PHYTOCHEMICAL AND IN VITRO ANTIOXIDANT STUDIES OF PRIMULA VERIS (L.) GROWING WILD IN KOSOVO
Ibrahim Rudhani, Florentina Raci, Hamide Ibrahimi, Arben Mehmeti, Ariana Kameri, Fatmir Faiku, Majlinda Daci, Sevdije Govori, Arben Haziri
ПЕДАГОГИЧЕСКА ПОЕМА
Преди година-две заедно с директора на Националното издателство „Аз- буки“ д-р Надя Кантарева-Барух посетихме няколко училища в Родопите. В едно от тях ни посрещнаха в голямата учителска стая. По стените ѝ имаше големи портрети на видни педагози, а под тях – художествено написани умни мисли, които те по някакъв повод са казали. На централно място бе портретът на Антон Семьонович Макаренко (1888 – 1939). Попитах учителките кой е Макаренко – те посрещнаха въпроса ми с мълчание. А някога, в г
Книжка 4
ИНТЕЛЕКТУАЛНАТА РЕФЛЕКСИЯ НА 15 – 17-ГОДИШНИ УЧЕНИЦИ В ОБУЧЕНИЕТО ПО „БИОЛОГИЯ И ЗДРАВНО ОБРАЗОВАНИЕ“: НИВА И ТЕНДЕНЦИИ НА РАЗВИТИЕ
Иса Хаджиали, Теодора Коларова
CHIMERICAL GROUPS IN SCHOOL AS A SOCIAL AND EDUCATIONAL PHENOMENON
Nikolay Tsankov, Veska Guyviiska
„СИМВОЛНИЯТ КАПИТАЛ“ НА БЪЛГАРСКОТО УЧИЛИЩЕ
Николай Цанков, Веска Гювийска
WEB-BASED DIAGNOSTIC TEST: INTRODUCING ISOMORPHIC ITEMS TO ASSESS STUDENTS’ MISCONCEPTIONS AND ERROR PATTERNS
Sentot Kusairi, Arif Hidayat, Nurul Hidayat
KINETICS OF PHOTO-ELECTRO-ASSISTED DEGRADATION OF REMAZOL RED 5B
Fitria Rahmawati, Tri Martini, Nina Iswati
COMPARISON STUDY OF DIFFERENT INORGANIC SILICA BASED REINFORCEMENT KAOLIN AND 3-GLYCYDILOXYPROPYLTRIMETHOXYSILANEON MECHANICAL, WATER UPTAKE AND SWELLING AREA PROPERTIES OF CHITOSAN COMPOSITES
Ozi A. Saputra, Windy A. Lestari, Dheo A. Saputra, Kartika S. Rini, Edi Pramono
SIMPLE TECHNIQUE FOR DETERMINING THE FORWARD RATE CONSTANT OF REVERSIBLE REACTION
Maulidan Firdaus, Patiha, Triana Kusumaningsih
ЗАБРАВЕНИ БЪЛГАРСКИ УЧИТЕЛИ: СИМЕОН ХРИСТОВ
Б. В. Тошев
ALLELOPATHIC AND IN VITRO ANTICANCER ACTIVITY OF STEVIA AND CHIA
Asya Dragoeva, Vanya Koleva, Zheni Stoyanova, Eli Zayova, Selime Ali
NOVEL HETEROARYLAMINO-CHROMEN-2-ONES AND THEIR ANTIBACTERIAL ACTIVITY
Ramiz Hoti, Naser Troni, Hamit Ismaili, Gjyle Mulliqi-Osmani, Veprim Thaçi
ONE DECADE OF THE “LUSI” MUD VOLCANO: PHYSICAL, CHEMICAL, AND GEOLOGICAL DIMENSIONS
Nadi Suprapto, Akhmad Zamroni, Eri Andrian Yudianto
Книжка 3
PERCEPTION OF PRESERVICE SCIENCE TEACHERS IN THE CONSTRUCTIVIST SCIENCE LEARNING ENVIRONMENT
Prasart Nuangchalerm, Jiří Dostál
ИНТЕРАКТИВНИ МЕТОДИ И ВЪЗМОЖНОСТИ ЗА ПРИЛОЖЕНИЕТО ИМ В ОБУЧЕНИЕТО ПО „БИОЛОГИЯ И ЗДРАВНО ОБРАЗОВАНИЕ“, VІІ КЛАС, С ЦЕЛ ЗДРАВНО ВЪЗПИТАНИЕ НА УЧЕНИЦИТЕ
Мария Бойчева, Росица Давидова, Силвия Маринова
ENHANCING THAI STUDENTS’ THINKING SKILLS ABOUT ENERGY ISSUES: INFLUENCE OF LOCAL VALUES
Chokchai Yuenyong
LIQUID-LIQUID EXTRACTION AND SPECTROPHOTOMETRIC CHARACTERIZATION OF SOME NEW ION-ASSOCIATED COMPLEXES OF Co(II) WITH INT: APPLICATION OF THE DEVELOPED METHOD FOR ANALYSIS OF SOIL COBALT CONTENT
L. Dospatliev, M. Ivanova
Quantum Connement of Mobile Na+ Ions in Sodium Silicate Glassy
QUANTUM CONFINEMENT OF MOBILE Na + IONS, IN SODIUM SILICATE GLASSY NANOPARTICLES
CONSERVATION OF THE UPSTREAM OPEN READING FRAMES IN THE GENES FOR THE ERB-B2 RECEPTOR TYROSINE KINASE 2 IN VERTEBRATES
Luchezar Karagyozov
OPTIMIZATION OF ENGINE OIL FORMULATION USING RESPONSE SURFACE METHODOLOGY AND GENETIC ALGORITHM: A COMPARATIVE STUDY
Behnaz Azmoon, Abolfazl Semnani, Ramin Jaberzadeh Ansari, Hamid Shakoori Langeroodi, Mahboube Shirani, Shima Ghanavati Nasab
EVALUATION OF ANTIBACTERIAL ACTIVITY OF DIFFERENT SOLVENT EXTRACTS OF TEUCRIUM CHAMAEDRYS (L.) GROWING WILD IN KOSOVO
Arben Haziri, Fatmir Faiku, Roze Berisha, Ibrahim Mehmeti, Sevdije Govori, Imer Haziri
QUALITY ASSESSMENT OF SUPPLY WATER OF GJAKOVA CITY (KOSOVO): A CASE STUDY OF CORRELATION COEFFICIENTS BETWEEN CHEMICAL DATA
Fatbardh Gashi, Naser Troni, Albert Maxhuni, Albana Mehmeti, Jeton Shabani
Книжка 2
ON THE PLACEMENT OF HYDROGEN AND HELIUM IN THE PERIODIC SYSTEM: A COMMENT
Julijana Cvetković, Vladimir M. Petruševski
USE OF COMPETENCE ONTOLOGICAL MODEL FOR MATCHING OF QUALIFICATIONS
J. Rogushina, S. Priyma
COMPUTER SIMULATORS: APPLICATION FOR GRADUATES’ADAPTATION AT OIL AND GAS REFINERIES
Irena O. Dolganova, Igor M. Dolganov, Kseniya A. Vasyuchka
BOSON/FERMION JANUS PARTICLES
Roumen Tsekov
АКТИВИРАЩА ЕНЕРГИЯ
Б. В. Тошев
SYNTHESIS, CHARACTERIZATION AND BIOLOGICAL ACTIVITIES OF PYRAZOLYL COPPER(II) NITRATE COMPLEXES
Munyaneza, G. Kumar, I. C. Morobe
SYNTHESIS OF NEW [(3-NITRO-2-OXO-2H-CHROMEN4-YLAMINO)-PHENYL]-PHENYL-TRIAZOLIDIN-4-ONES AND THEIR ANTIBACTERIAL ACTIVITY
Ramiz Hoti, Hamit Ismaili, Idriz Vehapi, Naser Troni, Gjyle Mulliqi-Osmani, Veprim Thaçi
STABILITY OF RJ-5 FUEL
Lemi Türker, Serhat Variş
A STUDY OF BEGLIKTASH MEGALITHIC COMPLEX
Diana Kjurkchieva, Evgeni Stoykov, Sabin Ivanov, Borislav Borisov, Hristo Hristov, Pencho Kyurkchiev, Dimitar Vladev, Irina Ivanova
Книжка 1
ЗА УСПЕШНО ОБРАЗОВАНИЕ FOR SUCCESSFUL EDUCATION
Б. В. Тошев
HIGHER EDUCATION PERSPECTIVES FOR AN EXCITING EDUCATIONALEXPERIENCE – PARTVII: AN INDIAN CONTEXT
B. H. S. Thimmappa
SCIENCE CAN BE FUN – MURPHY’S LAW AND HUMOUR IN NATURAL SCIENCE
Milan D. Stojković
ASSESSING LEVELS OF CO 2, CO, NO X AND SO 2 IN INDOOR AIR USING DRÄGER SENSORS: A CASE STADY IN PRISHTINA, KOSOVO
Shyqri Dumani, Fatbardh Gashi, Naser Troni
SYNTHESIS AND CHARACTERIZATION OF COMPOUND PMPA USING NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY AND OPTIMIZED MOLECULAR STRUCTURES CALCULATED USING THE DFT/B3LYP METHOD WITH THE 3-21G** BASIS SET COMBINED WITH THE Co II COMPLEX
Mohammad Mahdi Akbarzadeh, Khirollah Mehrani, Shahriar Ghammamy, Vahideh Hadigheh Rezvan
CARL FRIEDRIECH RAMMELSBERG AND THE EARLY DIFFUSION OF THE PERIODIC TABLE OF DMITRI MENDELEEV
Pierre-Léonard Zaffalon
2016 година
Книжка 6
ОТНОСНО ЕДНАКВАТА УПОТРЕБА НА ОСНОВНИТЕ ПОНЯТИЯ В ОБРАЗОВАНИЕТО И ОБУЧЕНИЕТО
Александър Ат. Панайотов
K DOES NOT PLAY THE ROLE OF THE
Juan Quílez
ЗАДАЧИ ОТ СМЕСЕН ТИП (BLENDED LEARNING) ЗА КУРС МЕТОДИКА НА ОБУЧЕНИЕТО ПО АНГЛИЙСКИ ЕЗИК (ЗА БИОЛОЗИ)
Анелия Кременска
ПРЕВРЪЩАНЕ НА ОБУЧЕНИЕТО ПО АСТРОНОМИЯ В РЕАЛЕН НАУЧНОИЗСЛЕДОВАТЕЛСКИ ПРОЦЕС – ИНОВАЦИЯ В ОБУЧЕНИЕТО
В. Радева, Д. Kюркчиева, Д. Димитров, Г. Борисов
SYNTHESIS AND CHARACTERIZATION OF PALLADIUM COMPLEXES OF SOME N,N,N’,N’- TETRAKIS(2-PYRIDYLMETHYL)ALKANEDIAMINE LIGANDS
Olayinka A. Oyetunji, Florence M. Nareetsile, Ruth Gontse, Lesedi Sheleng
A NEW APPROACH FOR THE SYNTHESIS OF P-ANISYL ETHYL FUMARATE: A C-9154 ANTIBIOTIC ANALOGUE
Maulidan Firdaus, Ahmad Ainurofiq, Aulia Vellarani
ДДТ – ВЕЩЕСТВОТО, КОЕТО Е ПОСРЕЩНАТО КАТО СПАСЕНИЕ, А ДНЕС СЕ НАМИРА В СПИСЪКА НА ЗАБРАНЕНИТЕ ВЕЩЕСТВА
Ивелин Кулев
THE EFFECT OF KOH AND KCL ADDITION TO THE DESTILATION OF ETHANOL-WATER MIXTURE
Khoirina Dwi Nugrahaningtyas, Fitria Rahmawati, Avrina Kumalasari
ПЪРВИТЕ ГОДИНИ НА ФИЗИКОХИМИЯТА В БЪЛГАРИЯ
Б. В. Тошев
Книжка 5
ПОСТИГАНЕТО НА ОБРАЗОВАТЕЛНИЯ МИНИМУМ И НОВИТЕ УЧЕБНИ ПРОГРАМИ ПО ГЕОГРАФИЯ В ПРОГИМНАЗИАЛНИЯ ЕТАП НА БЪЛГАРСКОТО УЧИЛИЩЕ
Иван Дреновски
ТЕНДЕНЦИИ НА ИЗСЛЕДВАНИЯТА В ПРИРОДОНАУЧНОТО ОБРАЗОВАНИЕ: КОНТЕНТ-АНАЛИЗ НА БЪЛГАРСКИ ПЕДАГОГИЧЕСКИ СПИСАНИЯ ОТ 2011 ДО 2015 Г.
Иса Хаджиали, Теодора Коларова
USE OF VECTORS AND FACTORIALS FOR CALCULATION OF MICROSTATES FROM P
M. Ivanova, L. Dospatliev
COLLEGE STUDENTS’ CONCEPTIONS OF NEWTONIAN MECHANICS: A CASE OF SURABAYA STATE UNIVERSITY INDONESIA
Nadi Suprapto, Dimas A. Syahrul, Seftyan Agustihana
ESTIMATION OF IGNITION TEMPERATURE FOR TWO KINDS OF ENERGETIC MATERIALS BY THERMAL ANALYSIS AND KINETIC EVALUATIONS
Mohammad Reza Nayeb-Hosseini, Mohammad Ferdowsi
SPECTROSCOPIC STUDIES ON A POTENTIAL COMPLEX BETWEEN TNT AND FOLIC ACID: A DFT STUDY
Lemi Türker, Serhat Variş
QUALITY ASSESSMENT AND CORRELATION COEFFICIENTS STUDY OF CHEMICAL PARAMETERS OF THE WELL WATER OF PLESHINA (KOSOVA)
F. Gashi, F. Faiku, N. Troni , A. Gashi
QUALITY ASSESSMENT OF RIVER WATER OF GRAQANICA (KOSOVO) AND CORRELATION STUDY OF CHEMICAL DATA
F. Gashi, N. Troni, R. Hoti, L. Latifi, V. Kolshi, A. Gashi
ОЦЕНЯВАНЕ ЛИЧНОСТТА НА УЧЕНИКА
Министерството на народното просвещение е направило допълне- ния към Правилника за гимназиите (ДВ, бр. 242 от 30 октомври 1941 г.), според които в бъдеще ще се оценяват следните прояви на учениците: (1) трудолюбие; (2) ред, точност и изпълнителност; (3) благовъзпитаност; (4) народностни прояви. Трудолюбието ще се оценява с бележките „образцово“, „добро“, „незадо- волително“. С „образцово“ ще се оценяват учениците, които с любов и по- стоянство извършват всяка възложена им ил
Книжка 4
INVESTIGATING PRESERVICE SECONDARY SCHOOL SCIENCE TEACHERS’ PRACTICES ABOUT INQUIRY-BASED INSTRUCTION DURING SCHOOL PRACTICUM
Prasart Nuangchalerm, Jiří Dostál, Xingkai Luo
HIGHER EDUCATION PERSPECTIVES FOR AN EXCITING EDUCATIONAL EXPERIENCE – PART VI: AN INDIAN CONTEXT
B. H. S. Thimmappa
ON THE PLACEMENT OF HYDROGEN AND HELIUM IN THE PERIODIC SYSTEM: A NEW APPROACH
Martín Labarca, Akash Srivaths
ATTITUDES TOWARDS SIGNIFICANCE OF HEALTHY BODY WEIGHT AND ADIPOSE TISSUE FUNCTIONS AMONG BIOLOGY STUDENTS
Asya Dragoeva, Masha Radoslavova, Vanya Koleva, Zhaklin Bakalova
HIGH SCHOOL STUDENTS’ MISCONCEPTIONS ABOUT MAGNETISM
Refik Dilber, Fatma Nur Ersoy
ПРИЛОЖЕНИЕ НА ИНТЕРАКТИВНИ МЕТОДИ ЗА ЕКОЛОГИЧНО И ЗДРАВНО ОБРАЗОВАНИЕ НА УЧЕНИЦИТЕ В VІІІ КЛАС ПО „БИОЛОГИЯ И ЗДРАВНО ОБРАЗОВАНИЕ“
Майя Радева, Мария Бойчева, Росица Давидова
ПРИЛОЖЕНИЕ НА ИНОВАЦИОННИ МЕТОДИ ЗА ЕКОЛОГИЧНО И ЗДРАВНО ОБРАЗОВАНИЕ И ВЪЗПИТАНИЕ НА УЧЕНИЦИТЕ В ОБУЧЕНИЕТО ПО БИОЛОГИЯ
Стойна Илиева, Мария Бойчева, Росица Давидова
VOLTAMMERIC SENSOR FOR NITROPHENOLS BASED ON SCREEN-PRINTED ELECTRODE MODIFIED WITH REDUCED GRAPHENE OXIDE
Arsim Maloku, Liridon S. Berisha, Granit Jashari, Eduard Andoni, Tahir Arbneshi
Книжка 3
ОТНОСНО ИМЕТО НА 114-ИЯ ЕЛЕМЕНТ
Ивелин Кулев
ИНТУИЦИЯ И ВЪОБРАЖЕНИЕ В НАУЧНИТЕ ИЗСЛЕДВАНИЯ
Д. Клисурски
СРАВНЯВАНЕ НА ОБРАЗОВАТЕЛНИТЕ И КАРИЕРНИТЕ ЦЕЛИ, ОЧАКВАНИЯ И УМЕНИЯ НА ПЪРВОКУРСНИЦИ ОТ „ХИМИЯ“ И „ФАРМАЦИЯ“
Александрия Генджова
ИЗСЛЕДВАНЕ НА ПРОФЕСИОНАЛНО-ПЕДАГОГИЧЕСКАТА РЕФЛЕКСИЯ НА УЧИТЕЛЯ ПО БИОЛОГИЯ (ЧАСТ ПЪРВА)
Иса Хаджиали, Надежда Райчева, Наташа Цанова
ИЗСЛЕДВАНЕ НА ПРОФЕСИОНАЛНО-ПЕДАГОГИЧЕСКАТА РЕФЛЕКСИЯ НА УЧИТЕЛЯ ПО БИОЛОГИЯ (ЧАСТ ВТОРА)
Надежда Райчева, Иса Хаджиали, Наташа Цанова, Виктория Нечева
SIGNIFICANCE OF THE INTERACTIVE CLINICAL CASES WITH VIRTUAL PATIENTS FOR LEARNING MEDICAL BIOCHEMISTRY
Ganka Kossekova, Tanya Monova, Bilyana Georgieva
EXISTING NATURE OF SCIENCE TEACHING OF A THAI IN-SERVICE BIOLOGY TEACHER
Wimol Sumranwanich, Sitthipon Art-in, Panee Maneechom, Chokchai Yuenyong
METEORITE HUNTING AND PHYSICS EDUCATION
Georgi N. Golemshinski
ASSESSMENT OF THE QUALITIES OF TEACHING EXPERIMENTS WHICH ILLUSTRATE THE GREENHOUSE EFFECT
Antoaneta Angelacheva
THE INFLUENCE OF THE NATURAL SCIENCES COMPONENT OF EDUCATION CONTENT ON THE EDUCATIONAL PROCESS ORGANIZATION IN UKRAINIAN SCHOOLS OF GENERAL EDUCATION IN THE SECOND HALF OF THE 19
M. M. Holovkova, A. A. Korobchenko
NUTRIENT COMPOSITION OF CUCURBITA MELO GROWING IN KOSOVO
Fatmir Faiku, Arben Haziri, Fatbardh Gashi, Naser Troni
ЗА ВИНОТО В ДРЕВНОСТТА И ДНЕС
Ивелин Кулев
РЕЛАЦИЯТА „ОБРАЗОВАТЕЛНИ ПАРАДИГМИ – ИНФОРМАЦИОННИ И КОМУНИКАЦИОННИ ТЕХНОЛОГИИ“ В КОНТЕКСТА НА ЕЛЕКТРОННОТО ОБУЧЕНИЕ
Камелия Йотовска
НАГРАДИТЕ „ЗЛАТНА ДЕТЕЛИНА“ ЗА 2016 Г.
На 8 март 2016 г. в голямата зала на Националния политехнически музей в София фондация „Вигория“ връчи годишните си награди – почетен плакет „Златна детелина“. Тази награда се дава за цялостна професионална и творче- ска изява на личности с особени заслуги към обществото в трите направления на фондация „Вигория“ – образование, екология, култура. Наградата цели да се даде израз на признателност за високи постижения на личности, които на професионално равнище и на доброволни начала са рабо
Книжка 2
MEDIATION IN RESOLVING CONFLICTS BETWEEN CHIMERIC SCHOOL GROUPS – A RESTORATIVE PRACTICE IN SCHOOL
Dobrinka Chankova, Nikolay Tsankov, Elina Popova
THE CONTRIBUTION OF MODEL TEACHING AND MATERIAL DEVELOPMENT TO PHYSICS TEACHING: FARADAY’S LAW OF INDUCTION
İbrahim Karaman, Refi k Dilber, Aydın Yelgün
THE NOVEL METHODS OF POLYMERIZATION AT HAND
Saâd Moulay
СТО ГОДИНИ ОТ РОЖДЕНИЕТО НА ПРОФЕСОР ХРИСТО ИВАНОВ (1916 – 2004)
СТО ГОДИНИ ОТ РОЖДЕНИЕТО, НА ПРОФЕСОР ХРИСТО ИВАНОВ, (96 – 00
CONTEXT-BASED CHEMISTRY LAB WORK WITH THE USE OF COMPUTER-ASSISTED LEARNING SYSTEM
N. Y. Stozhko, A. V. Tchernysheva, E.M. Podshivalova, B.I. Bortnik
VARIATION DEGREE IN E-LEARNING COURSES: ASSESSMENT THROUGH FEATURE MODELS
Ivo Damyanov, Nikolay Tsankov
Книжка 1
ПО ПЪТЯ
Б. В. Тошев
РАЗВИТИЕ НА УНИВЕРСИТЕТСКАТА ФИЗИКОХИМИЯ В ДВЕ ИСТОРИЧЕСКИ ЕПОХИ
Димо Платиканов
ПИКНОМЕТРИЧНО ОПРЕДЕЛЯНЕ НА КРИСТАЛНОСТ И ПОРЬОЗНОСТ В ПИРОКСЕНОВИ СТЪКЛОКЕРАМИКИ ОТ ПРОМИШЛЕНИ ОТПАДЪЦИ
Александра Камушева Александър Караманов
ИСТОРИЧЕСКИ КОРЕНИ И РАЗВИТИЕ НА КОНСТРУКТИВИЗМА
Адриана Тафрова-Григорова
INTERDISCIPLINARY PROJECT FOR ENHANCING STUDENTS’ INTEREST IN CHEMISTRY
Stela Georgieva, Petar Todorov , Zlatina Genova, Petia Peneva
ОЦЕНЯВАНЕ НА ВЪЗПРИЯТИЯТА ЗА УЧЕБНАТА СРЕДА В УНИВЕРСИТЕТСКИ ГРУПИ
Надя Илиева, Елена Бояджиева
2015 година
Книжка 6
HARD SPHERES MODEL OF THE ATOM
Roumen Tsekov
COMPLEX SYSTEMS FOR DRUG TRANSPORT ACROSS CELL MEMBRANES
Nikoleta Ivanova, Yana Tsoneva, Nina Ilkova, Anela Ivanova
SURFACE FUNCTIONALIZATION OF SILICA SOL-GEL MICROPARTICLES WITH EUROPIUM COMPLEXES
Nina Danchova , Gulay Ahmed , Michael Bredol , Stoyan Gutzov
STUDY OF PROTEIN MODIFIED GOLD NANOPARTICLES IN BULK PHASE AND AT AIR/WATER INTERFACE
A. Chanachev, P. Georgiev, Tz. Ivanova, K. Balashev
PARALLEL STABILITY ANALYSIS OF MEMBRANE LAMELLAR STRICTURES AND FOAM FILMS
Nikoleta G. Ivanova, Roumen Tsekov
INTERFACIAL REORGANIZATION OF MOLECULAR ASSEMBLIES USED AS DRUG DELIVERY SYSTEMS
I. Panaiotov, Tz. Ivanova, K. Balashev, N. Grozev, I. Minkov, K. Mircheva
ANOMALOUS DRAINAGE OF NANOFILMS FROM CONCENTRATED NACL SOLUTIONS OF TETRAETHYLENE GLYCOL OCTYL ETHER (C8E4)
Stoyan I. Karakashev
KINETICS OF THE OSMOTIC PROCESS AND THE POLARIZATION EFFECT
Boryan P. Radoev, Ivan L. Minkov, Emil D. Manev
WETTING BEHAVIOR OF A NATURAL AND A SYNTHETIC THERAPEUTIC PULMONARY SURFACTANTS
Lidia Alexandrova, Michail Nedyalkov, Dimo Platikanov
Книжка 5
TEACHER’S ACCEPTANCE OF STUDENTS WITH DISABILITY
Daniela Dimitrova-Radojchikj, Natasha Chichevska-Jovanova
‘SCIENTIFIC DISCIPLINES’ AWARENESS QUESTIONNAIRE
B.H.S. Thimmappa
SPECTRAL, MAGNETOCHEMICAL AND THERMO- GRAVIMETRIC ANALYSIS (TGA) OF TRANSITION METAL COMPLEXES WITH N^O TYPES LIGANDS
G. Kumar, A. Munyaneza, G. Ditsie
МУЛТИМЕДИЙНИТЕ ТЕСТОВЕ ПО ГЕОГРАФИЯ
Иван Дреновски
ДИСТАНЦИОННИТЕ АСТРОНОМИЧЕСКИ НАБЛЮДЕНИЯ – ИНОВАЦИЯ В ОБУЧЕНИЕТО ПО АСТРОНОМИЯ
В. Радева, Д. Kюркчиева, Д. Димитров, Г. Борисов
IRANIAN UNIVERSITY STUDENTS’ PERCEPTION OF CHEMISTRY LABORATORY ENVIRONMENTS
Zahra Eskandari, Nabi.A Ebrahimi Young Researchers & Elite Club, Arsanjan Branch,
APPLICATION OF LASER INDUCED BREAKDOWN SPECTROSCOPY AS NONDESDUCTRIVE AND SAFE ANALYSIS METHOD FOR COMPOSITE SOLID PROPELLANTS
Amir Hossein Farhadian, Masoud Kavosh Tehrani, Mohammad Hossein Keshavarz, Seyyed Mohamad Reza Darbany, Mehran Karimi, Amir Hossein Rezayi Optics & Laser Science and Technology Research Center,
THE EFFECT OF DIOCTYLPHTHALATE ON INITIAL PROPERTIES AND FIELD PERFORMANCE OF SOME SEMISYNTHETIC ENGINE OILS
Azadeh Ghasemizadeh, Abolfazl Semnani, Hamid Shakoori Langeroodi, Alireza Nezamzade Ejhieh
QUALITY ASSESSMENT OF RIVER’S WATER OF LUMBARDHI PEJA (KOSOVO)
Fatmir Faiku, Arben Haziri, Fatbardh Gashi, Naser Troni
ПРИЛОЖЕНИЕ НА ИНФОРМАЦИОННИТЕ И КОМУНИКАЦИОННИ ТЕХНОЛОГИИ В ОБУЧЕНИEТО ПО ХИМИЯ: МНЕНИЯ НА УЧИТЕЛИ ПО ХИМИЯ ОТ ЕДИН РЕГИОН В БЪЛГАРИЯ
Милена Кирова, Нели Костова, Милка Трендафилова
Книжка 4
БЛАГОДАРЯ ВИ!
Александър Панайотов
ПРИЗНАНИЕ ЗА ЕДНА ЧУДЕСНА НАУЧНА ДИСЦИПЛИНА
Васил Симеонов
USE OF OXIDATION NUMBERS FOR PREDICTING REGIOSELECTIVITY IN ORGANIC REACTIONS
Maulidan Firdaus, Patiha
ДЕКОМПОЗИЦИЯ НА ЕЛЕМЕНТИ ОТ СИСТЕМАТА ЗА УПРАВЛЕНИЕ НА КАЧЕСТВОТО НА СОФИЙСКИЯ УНИВЕРСИТЕТ В ПРОФЕСИОНАЛНАТА ПОДГОТОВКА НА УЧИТЕЛЯ ПО БИОЛОГИЯ
Наташа Цанова, Иса Хаджиали, Надежда Райчева
ТЕМАТА ВЪГЛЕХИДРАТИ В ПРОГРАМИТЕ ПО ХИМИЯ И БИОЛОГИЯ
Радка Томова, Елена Бояджиева, Миглена Славова , Мариан Николов
ЗА ПОКАЗАТЕЛНАТА ФУНКЦИЯ, ЛОГАРИТМИЧНАТА ФУНКЦИЯ И ЧИСЛОТО e
Ивелина Коцева
BILINGUAL COURSE IN BIOTECHNOLOGY: INTERDISCIPLINARY MODEL
V. Kolarski, D. Marinkova, R. Raykova, D. Danalev, S. Terzieva
ПРОУЧВАНЕ МНЕНИЕТО НА УЧЕНИЦИ ЗА ПОДГОТОВКАТА ПО ХИМИЯ В УЧИЛИЩЕ
М. Шекерлийска, В. Димитрова
TEACHING AND LEARNING EFFICACY OF VIRTUAL LABORATORY PACKAGE ON SELECTED NIGERIAN SECONDARY SCHOOL PHYSICS CONCEPTS
Oluwole Caleb Falode, Samuel Adenubi Onasanya
ХИМИЧНИЯТ ОПИТ – НАУКА И ЗАБАВА
Елица Чорбаджийска, Величка Димитрова, Магдалена Шекерлийска, Галина Бальова, Методийка Ангелова
ЕКОЛОГИЯТА В БЪЛГАРИЯ
Здравка Костова
ЕКОЛОГИЧНИ ПРИКЛЮЧЕНИЯ ВЪВ ВРЕМЕТО
Васил Симеонов
Книжка 3
ПОСТНОРМАЛНАТА НАУКА – БЕЛЕЗИ И НОВИ ТЕНДЕНЦИИ
Б. В. Тошев
SYNTHESIS OF FLUORINATED HYDROXYCINNAMOYL DERIVATIVES OF ANTI-INFLUENZA DRUGS AND THEIR BIOLOGICAL ACTIVITY
Boyka Stoykova, Maya Chochkova, Galya Ivanova, Luchia Mukova, Nadya Nikolova, Lubomira Nikolaeva-Glomb, Pavel Vojtíšek, Tsenka Milkova, Martin Štícha, David Havlíček
SYNTHESIS AND ANTIVIRAL ACTIVITY OF SOME AMINO ACIDS DERIVATIVES OF INFLUENZA VIRUS DRUGS
Radoslav Chayrov, Vesela Veselinova, Vasilka Markova, Luchia Mukova, Angel Galabov, Ivanka Stankova
NEW DERIVATIVES OF OSELTAMIVIR WITH BILE ACIDS
Kiril Chuchkov, Silvia Nakova, Lucia Mukova, Angel Galabov, Ivanka Stankova
MONOHYDROXY FLAVONES. PART III: THE MULLIKEN ANALYSIS
Maria Vakarelska-Popovska, Zhivko Velkov
LEU-ARG ANALOGUES: SYNTHESIS, IR CHARACTERIZATION AND DOCKING STUDIES
Tatyana Dzimbova, Atanas Chapkanov, Tamara Pajpanova
INVESTIGATION OF THE ETHERIFICATION PROCESS UNDER MODEL MIXTURE
Yordanka Tasheva
MODIFIED QUECHERS METHOD FOR DETERMINATION OF METHOMYL, ALDICARB, CARBOFURAN AND PROPOXUR IN LIVER
I. Stoykova, T. Yankovska-Stefenova, L.Yotova, D. Danalev Bulgarian Food Safety Agency, Sofi a, Bulgaria
ORGANIC COMPOUNDS AS INHIBITORS FOR MILD STEEL IN 1 M H SO
T. Haralanova, C. Girginov
MICROBIAL X CELLS – INNOVATIVE MULTIPURPOSE BIOELECTROCHEMICAL SYSTEMS
Mario Mitov, Yolina Hubenova
LACTOBACILLUS PLANTARUM AC 11S AS A BIOCATALYST IN MICROBIAL ELECYTOLYSIS CELL
Elitsa Chorbadzhiyska, Yolina Hubenova, Sophia Yankova, Dragomir Yankov, Mario Mitov
Pd-Au DEPOSITES ON NI-FOAM AS ANODIC ELECTROCATALYSTS FOR DIRECT BOROHYDRIDE FUEL CELL
Georgi Hristov, Elitsa Chorbadzhiyska, Mario Mitov
SEDIMENT MICROBIAL FUEL CELLS AS POWER SOURCES FOR SMALL ELECTRICAL CONSUMERS
Ivo Bardarov, Yolina Hubenova, Mario Mitov
SOLID PHASE EXTRACTION OF Au(III) USING SILICA GEL MODIFIED WITH 4-AMINOANTIPYRINE SCHIFF BASES
P. Petrova, I. Karadjova, M. Chochkova, I. Dakova
INDUCTIVELY COUPLED PLASMA OPTICAL EMISSION SPECTROSCOPY – DETERMINATION OF RARE EARTH AND PLATINUM GROUP OF ELEMENTS
N. Velitchkova, P. Petrova, S. Velichkov, N. Daskalova
STUDYING THE PROCESS OF DEPOSITION OF ANTIMONY WITH CALCIUM CARBONATE
K. B. Omarov, Z. B. Absat, S. K. Aldabergenova, A. B. Siyazova, N. J. Rakhimzhanova, Z. B. Sagindykova
Книжка 2
АКАДЕМИЧНО СЛОВО ПРЕД АБСОЛВЕНТИТЕ ОТ ВИПУСК 2014
Скъпи колеги,
ЗА ИНТЕЛЕКТУАЛНИЯ „СИНЕРГИЗЪМ“ МЕЖДУ ДВА ЕВРОПЕЙСКИ ПРОЕКТА
INTELLECTUAL “SYNERGY” BETWEEN TWO EUROPEАN PROJECTS
TEACHING CHEMISTRY AT TECHNICAL UNIVERSITY
Lilyana Nacheva-Skopalik, Milena Koleva
ФОРМИРАЩО ОЦЕНЯВАНЕ PEER INSTRUCTION С ПОМОЩТА НА PLICКERS ТЕХНОЛОГИЯТА
Ивелина Коцева, Мая Гайдарова, Галина Ненчева
IMPROVING STUDENTS’ PERFORMANCE IN NAMING AND WRITING STRUCTURAL FORMULAE OF HYDROCARBONS USING THE BALL-AND-STICK MODELS
Peter Abum Sarkodie, Kenneth Adu-Gyamfi
STUDENT PERFORMANCE IN A SEMINAR BASED EXAMINATION OF BASIC BIOCHEMISTRY COURSE
Mohammed Elimam Ahamed Mohammed
VAPOR PRESSURES OF 1-BUTANOL OVER WIDE RANGE OF THEMPERATURES
Javid Safarov, Bahruz Ahmadov, Saleh Mirzayev, Astan Shahverdiyev, Egon Hassel
ДИЗАЙН НА УНИВЕРСИТЕТСКИ КУРС ЗА ЕЛЕКTРОННО ОБУЧЕНИЕ (ЗА БЪДЕЩИ УЧИТЕЛИ ПО БИОЛОГИЯ)
Камелия Йотовска
КУЛТУРНА ИСТОРИЯ НА НАУКАТА: НОВИ ИДЕИ ЗА МАТЕРИЯТА И ВЪЗНИКВАНЕТО НА МОДЕРНАТА ХИМИЯ
CULTURAL HISTORY OF SCIENCE: NEW IDEAS FOR THE MATTER AND THE EMERGENCE OF MODERN CHEMISTRY
Книжка 1
ТРЕВОЖНОСТТА В ЧАСОВЕТЕ ПО ПРИРОДНИ НАУКИ
Здравка Костова
НОМЕНКЛАТУРНИ ПРЕПОРЪКИ НА МЕЖДУНАРОДНИЯ СЪЮЗ ПО ЧИСТА И ПРИЛОЖНА ХИМИЯ (IUPAC), СВЪРЗАНИ С ХИМИЧНАТА ТЕРМИНОЛОГИЯ И ВЕЛИЧИНИ, ЕДИНИЦИ И СИМВОЛИ, ИЗПОЛЗВАНИ В ХИМИЯТА
Александър Захариев
HIGHER EDUCATION PERSPECTIVES FOR AN EXCITING EDUCATIONAL EXPERIENCE – PART V: AN INDIAN CONTEXT
B. H. S. Thimmappa
ГРАФИЧНИ ЗАДАЧИ В ОБУЧЕНИЕТО ПО ФИЗИКА В СРЕДНОТО УЧИЛИЩЕ
Христина Петрова
РУМЕН ЛЮБОМИРОВ ДОЙЧЕВ (1938 – 1999)
Огнян Димитров, Здравка Костова
BRAIN-LIKE SPATIO-TEMPORAL DATA MACHINES
N. Kasabov
НАУЧНИТЕ ИЗСЛЕДВАНИЯ ПО ХИМИЯ В СОФИЙСКИЯ УНИВЕРСИТЕТ „СВ. КЛИМЕНТ ОХРИДСКИ“ ПРЕЗ ПЪРВОТО ИМ СТОЛЕТИЕ1)
Димо Платиканов
NAMING OF CHEMICAL ELEMENTS
Maria Atanassova
НАЙДЕН НАЙДЕНОВ, 1929 – 2014 СПОМЕН ЗА ПРИЯТЕЛЯ
ИНЖ. НАЙДЕН ХРИСТОВ НАЙДЕНОВ, СЕКРЕТАР, НА СЪЮЗА НА ХИМИЦИТЕ В БЪЛГАРИЯ (2.10.1929 – 25.10.2014)
2014 година
Книжка 6
145 ГОДИНИ БЪЛГАРСКА АКАДЕМИЯ НА НАУКИТЕ
145 ANNIVERSARY OF THE BULGARIAN ACADEMY OF SCIENCES
SERVICE LEARNING IN SCIENCE TEACHER PREPARATION PROGRAM: CONCEPTS AND PRACTICES
Prasart Nuangchalerm
ПАРНО НАЛЯГАНЕ НА РАЗТВОРИ
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
IMPROVEMENT OF STEM EDUCATION WITH THE INTEGRATION OF DATA-LOGGERS IN THE SHINING STAR PROJECT, 2007-2011 IN SOUTHERN INDIANA
James E. Hollenbeck
АСТРОНОМИЧЕСКИЯТ ОБРАЗОВАТЕЛЕН ПРОЕКТ „MY KEPLER“ – ВРЪЗКА МЕЖДУ НАУКАТА И ОБРАЗОВАНИЕТО
В. Радева, Д. Kюркчиева, Д. Димитров
EFFECT OF STUDENTS’ BACKGROUND KNOWLEDGE OF MATHEMATICS ON SENIOR SECONDARY SCHOOL STUDENTS’ ACHIEVEMENT IN PHYSICS
Ayodele Ogunleye, Adeneye O. A. Awofala, Emiola A. Adekoya
SYNTHESIS AND CHARACTERIZATION OF MIXED LIGAND CO(II) AND NI(II) COMPLEXES WITH L- PHENYLALANINE AND HIPPURIC ACID
G. Kumar, A. Munyaneza, G. Ditsie
LUBRICATION PROPERTIES OF DIFFERENT PENTAERYTHRITOL-OLEIC ACID REACTION PRODUCTS
Abolfazl Semnani, Hamid Shakoori Langeroodi, Mahboube Shirani
THE ORIGINS OF SECONDARY AND TERTIARY GENERAL EDUCATION IN RUSSIA: HISTORICAL VIEWS FROM THE 21ST CENTURY
V. Romanenko, G. Nikitina Academy of Information Technologies in Education, Russia
ALLELOPATHIC AND CYTOTOXIC ACTIVITY OF ORIGANUM VULGARE SSP. VULGARE GROWING WILD IN BULGARIA
Asya Pencheva Dragoeva, Vanya Petrova Koleva, Zheni Dimitrova Nanova, Mariya Zhivkova Kaschieva, Irina Rumenova Yotova
ХЕМОМЕТРИЯТА И ПРОФЕСОР ВАСИЛ СИМЕОНОВ
CHEMOMETRY AND PROFESSOR VASSIL SIMEONOV
ПРОЕКТЪТ ЗА ЕЛЕКТРОННО ОБУЧЕНИЕ ВЪВ ФАКУЛТЕТА ПО ХИМИЯ И ФАРМАЦИЯ НА СОФИЙСКИЯ УНИВЕРСИТЕТ „СВ. КЛИМЕНТ ОХРИДСКИ“
Стефан Цаковски, Васил Симеонов
Книжка 5
ЗА ДОСТОВЕРНОСТТА НА ИНТЕРНЕТ УРОЦИТЕ ПО ГЕОГРАФИЯ
FOR RELIABILITY OF INTERNET LESSONS IN GEOGRAPHY
GENDER ISSUES OF UKRAINIAN HIGHER EDUCATION
Н.H.Petruchenia, M.I.Vorovka
ПАРНО НАЛЯГАНЕ НА ТЕЧНОСТИ
Б. В. Тошев
HIGHER EDUCATION PERSPECTIVES FOR AN EXCITING EDUCATIONAL EXPERIENCE – PART IV – AN INDIAN CONTEXT
B. H. S. Thimmappa
МНОГОВАРИАЦИОННА СТАТИСТИЧЕСКА ОЦЕНКА НА DREEM – БЪЛГАРИЯ: ВЪЗПРИЕМАНЕ НА ОБРАЗОВАТЕЛНАТА СРЕДА ОТ СТУДЕНТИТЕ В МЕДИЦИНСКИЯ УНИВЕРСИТЕТ – СОФИЯ
Радка Томова, Павлина Гатева, Радка Хаджиолова, Зафер Сабит, Миглена Славова, Гергана Чергарова, Васил Симеонов
FACTORS DETERMINING THE IMPROVEMENT OF EDUCATION QUALITY OF FOREIGN STUDENTS IN THE MEDICAL UNIVERSITY
Stoyanka Lazarova Kokova
МОДЕЛ И ТЕХНОЛОГИЯ НА ОБУЧЕНИЕ В ЛАБОРАТОРНИТЕ УПРАЖНЕНИЯ ПО ДИСЦИПЛИНАТА „ФИЗИОЛОГИЯ НА ЖИВОТНИТЕ И ЧОВЕКА“ С ПРИЛОЖЕНИЕ НА ВИРТУАЛНИ ЕКСПЕРИМЕНТИ
Маша Радославова, Мария Бойчева
MUSSEL BIOADHESIVES: A TOP LESSON FROM NATURE
Saâd Moulay Université Saâd Dahlab de Blida, Algeria
THE ROLE OF GREEN PESTICIDES FOR SUSTAINABLE GREEN ECONOMY
Bizuneh Adinew
Книжка 4
ЕЛЕКТРОННО ПОМАГАЛO „ОТ АТОМА ДО КОСМОСА“ ЗА УЧЕНИЦИ ОТ Х КЛАС
Силвия Боянова Професионална гимназия „Акад. Сергей П. Корольов“ – Дупница
CONVENTIONAL TEACHING VERSUS POWER POINT PRESENTATION: A COMPARATIVE STUDY FOR UNDERGRADUATE ORGANIC CHEMISTRY STUDENTS
Sunena Chandra, Ram N. Yadav, Bimal K. Banik
ЕСЕТО КАТО ИНТЕГРАТИВЕН КОНСТРУКТ – НОРМАТИВЕН, ПРОЦЕСУАЛЕН И ОЦЕНЪЧНО-РЕЗУЛТАТИВЕН АСПЕКТ
Надежда Райчева, Иван Капурдов, Наташа Цанова, Иса Хаджиали, Снежана Томова
ISOLATION AND CHARACTERIZATION OF COLLAGEN FROM THE SKIN OF SYRIAN SHEEP
Manar Abu-Hassan, Ahmad Malo
ФОРМИРАНЕ НА ГРАФИЧНИ ЗНАНИЯ И УМЕНИЯ У УЧЕНИЦИТЕ ПРИ РЕШАВАНЕ НА ФИЗИЧНИ ЗАДАЧИ С ГРАФИЧЕН МЕТОД
Христина Петрова
ЗАДАЧАТА В КОНТЕКСТА НА РЕФЛЕКСИВНА ТЕХНОЛОГИЯ ЗА ОБУЧЕНИЕ ПО БИОЛОГИЯ
Иса Хаджиали, Надежда Райчева, Наташа Цанова
44
Донка Ташева, Пенка Василева
AB INITIO STUDY ON STRUCTURAL PROPERTIES AND VIBRATIONAL ANALYSIS OF Z-(1-PYRIDIN-2-YL-METHYLENE)- THIOSEMICARBAZONE COMPOUND
Mohammad Mehdi Akbarzadeh, Hajar Sahebalzamani
ДОЦ. Д.П.Н. АЛЕКСАНДЪР АТАНАСОВ ПАНАЙОТОВ
Наташа Цанова, Иса Хаджиали, Надежда Райчева
COMPUTER ASSISTED LEARNING SYSTEM FOR STUDYING ANALYTICAL CHEMISTRY
N. Y. Stozhko, A. V. Tchernysheva, L.I. Mironova
С РАКЕТНА ГРАНАТА КЪМ МЕСЕЦА: БОРБА С ЕДНА ЛЕДЕНА ЕПОХА В ГОДИНАТА 3000 СЛЕД ХРИСТА. 3.
С РАКЕТНА ГРАНАТА КЪМ МЕСЕЦА:, БОРБА С ЕДНА ЛЕДЕНА ЕПОХА, В ГОДИНАТА 000 СЛЕД ХРИСТА. .
Книжка 3
ДМИТРИ ИВАНОВИЧ МЕНДЕЛЕЕВ – ГЕНИЙ НА ЧОВЕЧЕСТВОТО И ВЕЛИК РЕФОРМАТОР
DMITRI IVANOVICH MENDELEEV (1834 – 1907)
KNOWLEDGE OF AND ATTITUDES TOWARDS WATER IN 5
Antoaneta Angelacheva, Kalina Kamarska
ВИСША МАТЕМАТИКА ЗА УЧИТЕЛИ, УЧЕНИЦИ И СТУДЕНТИ: ДИФЕРЕНЦИАЛНО СМЯТАНЕ
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
EFFECTS OF THREE COOPERATIVE LEARNING STRATEGIES ON THE PERFORMANCE OF SECONDARY SCHOOL STUDENTS IN PHYSICS
Isiaka Amosa Gambari, Mudasiru Olalere Yusuf
STUDENTS’ METACOGNITIVE SELF- REGULATION – A CASE STUDY: MOLECULAR STRUCTURE PROBLEM SOLVING
Bambang Sugiarto, Prabowo, Suyono
TUNING THE ELECTRONIC PROPERTIES OF HETEROGENEOUS CATALYSTS: AN AUTHENTIC RESEARCH-BASED LABORATORY COURSE
Paweł Bernard, Gabriela Grzybek, Paweł Stelmachowski
ВАСИЛ ХРИСТОВ БОЗАРОВ
Пенка Бозарова, Здравка Костова
NEED TO LINK THE TWO CRUCIAL CONTEMPORARY STRATEGIES – SUSTAINABLE DEVELOPMENT AND INNOVATIVE ECONOMY
M. Lyubenova, G. Gushlekov, А. Assenov
AVAILABILITY AND TEACHERS’ AWARENESS OF THE EXISTENCE OF SOFTWARE PACKAGES FOR DEVELOPING PHYSICS INSTRUCTION FOR SECONDARY SCHOOL STUDENTS IN MINNA, NIGERIA
Оluwole Caleb Falode, Nasir Adewale Ajala
ЖИВАТА ПРИРОДА
LIVING NATURE
БИБЛИОГРАФИЯ НА СТАТИИ ЗА МИСКОНЦЕПЦИИТЕ В ОБУЧЕНИЕТО ПО ПРИРОДНИ НАУКИ ВЪВ ВСИЧКИ ОБРАЗОВАТЕЛНИ НИВА
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
Книжка 2
SCIENTIX – OБЩНОСТ ЗА НАУЧНО ОБРАЗОВАНИЕ В ЕВРОПА
Свежина Димитрова Народна астрономическа обсерватория и планетариум „Николай Коперник“ – Варна
ПЪТИЩА ЗА РАЗВИТИЕ НА ПОЗНАВАТЕЛНИЯ ИНТЕРЕС НА УЧЕНИЦИТЕ ПО ПРЕДМЕТА „ЧОВЕКЪТ И ПРИРОДАТА, VІ КЛАС: СТРУКТУРА И ЖИЗНЕНИ ПРОЦЕСИ НА ОРГАНИЗМИТЕ“ В КОНТЕКСТА НА КВАЛИФИКАЦИЯТА НА УЧИТЕЛИ БЕЗ БИОЛОГИЧНО ОБРАЗОВАНИЕ. III
Мария Бойчева, Росица Давидова
МЕЖДУПРЕДМЕТНИ ВРЪЗКИ НА АСТРОНОМИЯТА С ЛИТЕРАТУРАТА И ИНФОРМАЦИОННИТЕ ТЕХНОЛОГИИ
Н. Данкова, Р. Бенчева, И. Ковачев
ДИАГНОСТИКА НА ЕКОЛОГИЧНАТА КУЛТУРА НА УЧЕНИЦИТЕ ПРИ ИЗУЧАВАНЕ НА VI-А ГРУПА НА ПЕРИОДИЧНАТА ТАБЛИЦА В 8. КЛАС
Антоанета Ангелачева
HIGHER EDUCATION PERSPECTIVES FOR AN EXCITING EDUCATIONAL EXPERIENCE – PART III: AN INDIAN CONTEXT
B.H.S. Thimmappa
THERMODYNAMIC AND INTERFACIAL STUDIES ON CO-CRYSTALS OF NICOTINAMIDE - THIOUREA DRUG SYSTEM
Vishnu Kant, H. Shekhar
СРАВНИТЕЛНА ОЦЕНКА НА МЕТОДИТЕ ЗА ИЗРАВНЯВАНЕ НА ОКИСЛИТЕЛНО-РЕДУКЦИОННИ РЕАКЦИИ: ПРЕДИМСТВА И НЕДОСТАТЪЦИ
И. Л. Дуков
ГЕНЕРИЧНА НЕСТАБИЛНОСТ В МОДЕЛА НА ДИФУЗИОННО-КОНТРОЛИРАНА АГРЕГАЦИЯ (ДКА): ЕФЕКТ НА ГЛОБАЛНИТЕ РАДИУСИ НА ПОРАЖДАНЕ И ИЗОСТАВЯНЕ
Христина Попова, Десислава Петкова, Веселин Тончев
BOTYU ATANASSOV BOTEV
Zdravka Kostova, Margarita Topashka-Ancheva
CHRONOLOGY OF CHEMICAL ELEMENTS DISCOVERIES
Maria Atanassova, Radoslav Angelov
Книжка 1
ПРИРОДОНАУЧНА НЕГРАМОТНОСТ – КОНСТРУКТИВИЗЪМ – МИСКОНЦЕПЦИИ – ИСТОРИЧЕСКА ЧУВСТВИТЕЛНОСТ
Б. В. Тошев
ОБРАЗОВАНИЕ ЗА ПРИРОДОНАУЧНА ГРАМОТНОСТ
Адриана Тафрова-Григорова
A COMMENTARY ON THE GENERATION OF AUDIENCE-ORIENTED EDUCATIONAL PARADIGMS IN NUCLEAR PHYSICS
Baldomero Herrera-González Universidad Autónoma del Estado de México, Mexico
СТРАТЕГИИ ЗА МОТИВАЦИЯ В ОБУЧЕНИЕТО ПО ХИМИЯ, СВЪРЗАНИ СЪС СЪДЪРЖАНИЕТО НА ПРЕДМЕТА
Александрия Генджова
INCREASING STUDENTS’ INTEREST IN CHEMISTRY WITH CONTEXT-BASED APPROACHES FOR CONTROL AND ASSESSMENT IN THE ENGLISH LANGUAGE PROGRAM AT MEDICAL UNIVERSITY IN VARNA
Zlatina Peteva, Lubomir Makedonski, Mona Stancheva Medical Universicy, Varna
РЕЗУЛТАТИ ОТ ЕКСПЕРИМЕНТАЛНО ОБУЧЕНИЕ ПО МЕТОДИКА ЗА РЕФЛЕКСИВНО ИЗСЛЕДВАНЕ НА ХИМИЧНИ ОБЕКТИ (VI КЛАС)
Калина Камарска, Дарина Узова, Милка Голешова
ПРИМЕРЕН МОДЕЛ ЗА ОРГАНИЗИРАНЕ НА КЛУБНА ДЕЙНОСТ В СРЕДНОТО ОБЩООБРАЗОВАТЕЛНО УЧИЛИЩЕ
П. Галчева, А. Хинева
PURIFICATION OF ANILINE AND NITRO- SUBSTITUTED ANILINE CONTAMINANTS FROM AQUEOUS SOLUTION USING BETA ZEOLITE
Talib M. Albayati, Aidan M. Doyle
АНАЛИТИЧНАТА ХИМИЯ В БЪЛГАРИЯ: ПРОФЕСОР ДИМИТЪР ЦАЛЕВ
ANALYTICAL CHEMISTRY IN BULGARIA: PROFESSOR DIMITER TSALEV
АКАДЕМИК ДИМИТЪР КЛИСУРСКИ НА 80 ГОДИНИ
PROFESSOR DIMITER KLISSURSKI AT 80
КАК СА ПРЕПОДАВАНИ ПРИРОДНИТЕ НАУКИ В ПЕТОКЛАСНИТЕ ДЕВИЧЕСКИ УЧИЛИЩА И В ДОЛНИЯ КУРС НА ДЕВИЧЕСКИТЕ ГИМНАЗИИ (1897 Г.): ФИЗИКА И ХИМИЯ
TEACHING SCIENCE IN THE BULGARIAN SCHOOLS FOR GIRLS (1897): PHYSICS AND CHEMISTRY
2013 година
Книжка 6
УЧЕНИЧЕСКИ КЛУБ ПО ПЧЕЛАРСТВО BEEKEEPING CLUB AT SCHOOL
Златка Гарова
DIFFERENTIAL TEACHING IN SCHOOL SCIENCE EDUCATION: CONCEPTUAL PRINCIPLES
G. Yuzbasheva Kherson Academy of Continuing Education, Ukraine
АНАЛИЗ НА ПОСТИЖЕНИЯТА НА УЧЕНИЦИТЕ ОТ ШЕСТИ КЛАС ВЪРХУ РАЗДЕЛ „ВЕЩЕСТВА И ТЕХНИТЕ СВОЙСТВА“ ПО „ЧОВЕКЪТ И ПРИРОДАТА“
Иваничка Буровска, Стефан Цаковски Регионален инспекторат по образованието – Ловеч
ВЗАИМОДЕЙСТВИЕ НА ЖЕЛЯЗО С АЗОТНА КИСЕЛИНА: СЛОЖНА ОКИСЛИТЕЛНО-РЕДУКЦИОННА РЕАКЦИЯ
Александър Захариев
ТЕОРЕТИЧНО ИЗСЛЕДВАНЕ НА ИЗБОРА НА НЕЗАВИСИМИ ПАРАМЕТРИ ПРИ ОКИСЛИТЕЛНО-РЕДУКЦИОННИ РЕАКЦИИ С ПОВЕЧЕ ОТ ЕДНА СТЕПЕН НА СВОБОДА
Сашка Петкова, Мария Атанасова, Румяна Чуклева
PSYCHOSOCIAL ENVIRONMENT OF CHEMISTRY LABORATORY CLASSROOMS IN IRANIAN HIGH SCHOOLS
Zahra Eskandari, Nabi.A Ebrahimi
DENSITY FUNCTIONAL THEORY OF THE EFFICIENCIES OF 2-PHENYLIMIDAZO[1,2-A]PYRIDINE AND 2-(M-METHOXYPHENYL)IMIDAZO[1,2-A] PYRIMIDINE AS CORROSION INHIBITORS FOR MILD STEEL
Banjo Semire, Ayobami Olusegun Odunola
КАК СА ПРЕПОДАВАНИ ОБЩЕСТВЕНИТЕ НАУКИ В ПЕТОКЛАСНИТЕ ДЕВИЧЕСКИ УЧИЛИЩА И В ДОЛНИЯ КУРС НА ДЕВИЧЕСКИТЕ ГИМНАЗИИ (1897 Г.): НРАВОУЧЕНИЕ
TEACHING SOCIAL SCIENCES IN THE BULGARIAN SCHOOLS FOR GIRLS (1897): MORALITY
HISTORY AND PHILOSOPHY OF SCIENCE: SOME RECENT PERIODICALS (2013)
Chemistry: Bulgarian Journal of Science Education
45. НАЦИОНАЛНА КОНФЕРЕНЦИЯ НА УЧИТЕЛИТЕ ПО ХИМИЯ
„Образователни стандарти и природонаучна грамотност“ – това е темата на състоялата се от 25 до 27 октомври 2013 г. в Габрово 45. Национална конфе- ренция на учителите по химия с международно участие, която по традиция се проведе комбинирано с Годишната конференция на Българското дружество за химическо образование и история и философия на химията. Изборът на темата е предизвикан от факта, че развиването на природонаучна грамотност е обща тенденция на реформите на учебните програми и главна
Книжка 5
UNDERSTANDING THE CONCEPT OF DIGESTIVE SYSTEM IN BIOLOGY USING COMPUTER SIMULATION
A. I. Gambari, A. A. Yaki, T. T. Olowe
ФОРМИРАНЕ НА КЛЮЧОВИ КОМПЕТЕНТНОСТИ ЧРЕЗ ПРОБЛЕМНО БАЗИРАН ПОДХОД В ОБУЧЕНИЕТО ПО ХИМИЯ В СРЕДНОТО УЧИЛИЩЕ
Владимир Цветков, Елена Бояджиева
SNAPSHOT OF SCIENCE CLASSROOM TEACHING FROM THE POINT OF VIEW OF IDEAS OF CONSTRUCTIVISM: A CASE STUDY – SECONDARY SCHOOLS IN SOFIA, BULGARIA
James Hollenbeck, Milena Kirova, Elena Boiadjieva, Adriana Tafrova-Grigorova
ОБЯСНЕНИЕ НА ФАКТИ И ЯВЛЕНИЯ В ОБУЧЕНИЕТО ПО ХИМИЯ – КОНСТРУКТИВИСТКИ ПОДХОД
Йорданка Стефанова
МОДЕЛ НА РЕФЛЕКСИВЕН ПОДХОД В ГИМНАЗИАЛНИЯ ЕТАП НА БИОЛОГИЧНОТО ОБРАЗОВАНИЕ (IХ – ХI КЛАС)
Иса Хаджиали, Теодора Коларова
TWO INVESTIGATIONS OF EXAMINERS’ PERCEPTIONS OF PRIOR KNOWLEDGE REQUIRED FOR SOLVING STOICHIOMETRIC PROBLEMS AND ITS RELATIONSHIP TO STUDENTS’ PRIOR KNOWLEDGE
Ayoade Ejiwale Okanlawon
ЗА ХИМИЯТА НА БИРАТА
Ивелин Кулев
NOBEL LAUREATES IN CHEMISTRY FROM THE TERRITORY OF FORMER YUGOSLAVIA
Milan D. Stojković
МЕТЕОРИТЪТ ОТ БЕЛОГРАДЧИК
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
BINET CONSTRUCTION IN ONLINE STEREO 3D VISUALIZATION
S. Zabunov, M. Gaydarova
КАК СА ПРЕПОДАВАНИ ПРИРОДНИТЕ НАУКИ В ПЕТОКЛАСНИТЕ ДЕВИЧЕСКИ УЧИЛИЩА И В ДОЛНИЯ КУРС НА ДЕВИЧЕСКИТЕ ГИМНАЗИИ (1897 Г.): ЕСТЕСТВЕНА ИСТОРИЯ
TEACHING SCIENCE IN THE BULGARIAN SCHOOLS FOR GIRLS (1897): NATURAL HISTORY
Книжка 4
АНАЛИЗ НА РАЗМЕРНОСТИТЕ: ПРИМЕР ОТ ИЗСЛЕДВАНИЯТА ВЪРХУ ГРУПИРАНЕ НА СТЪПАЛА
DIMENSIONAL ANALYSIS: AN EXAPLE
RECASTING THE DERIVATION OF THE CLAPEYRON EQUATION INTO A CONCEPTUALLY SIMPLER FORM
Srihari Murthy Meenakshi Sundararajan Engineering College, India
CHEMICAL REACTIONS DO NOT ALWAYS MODERATE CHANGES IN CONCENTRATION OF AN ACTIVE COMPONENT
Joan J. Solaz-Portolés, Vicent Sanjosé Universitat de Valènciа, Spain
СЪВРЕМЕННИ ИЗИСКВАНИЯ КЪМ ПРОФЕСИОНАЛНАТА ПОДГОТОВКА НА ИНЖЕНЕРИ ПО ЕНЕРГЕТИКА
Надя Илиева, Елена Бояджиева
ДИДАКТИЧЕСКИ СРЕДСТВА ЗА ФОРМИРАНЕ И ДИАГНОСТИКА НА ЕКОЛОГИЧНАТА КУЛТУРА НА УЧЕНИЦИТЕ В ОБУЧЕНИЕТО ПО ХИМИЯ
Антоанета Ангелачева, Eлена Гергова
POLYMETALLIC COMPEXES: CV. SYNTHESIS, SPECTRAL, THERMOGRAVIMETRIC, XRD, MOLECULAR MODELLING AND POTENTIAL ANTIBACTERIAL PROPERTIES OF TETRAMERIC COMPLEXES OF Co(II), Ni(II), Cu(II), Zn(II), Cd(II) AND Hg(II) WITH OCTADENTATE AZODYE LIGANDS
Bipin B. Mahapatra, S. N. Dehury, A. K. Sarangi, S. N. Chaulia G. M. Autonomous College, India Covt. College of Engineering Kalahandi, India DAV Junior College, India
SYNTHESIS AND CHARACTERIZATION OF MIXED LIGAND Cu(II) AND Co(II) COMPLEXES OF L-PHENYLALANINE AND IMINODIACETIC ACID
G. Kumar , A. Munyaneza, G. Ditse
SCIENCE LITERACY IN THE FORMER YUGOSLAVIA: SCHOOL EDUCATIONAL PROGRAMS ON TV AND SCIENCTIFIC-POPULAR LITERATURE
Milan D. Stojković
СРАВНЯВАНЕ СВОЙСТВАТА НА СЪЕДИНЕНИЯ ПРИ D-ЕЛЕМЕНТИТЕ С АНАЛОГИЧНИ ПО БРОЙ НА ВАЛЕНТНИ ЕЛЕКТРОНИ СЪЕДИНЕНИЯ НА s- И р-ЕЛЕМЕНТИ
Елена Киркова
ПРОФЕСОР ЕЛЕНА КИРКОВА НАВЪРШИ 90 ГОДИНИ
CELEBRATING 90TH ANNIVERSARY OF PROFESSOR ELENA KIRKOVA
ВТОРИ ПРИНЦИП НА ТЕРМОДИНАМИКАТА: ЗАЩО ПРОЦЕСИТЕ В ПРИРОДАТ А И ОБЩЕСТВОТО СА НЕОБРАТИМИ?
Б. В. Тошев
КАК СА ПРЕПОДАВАНИ ПРИРОДНИТЕ НАУКИ В ПЕТОКЛАСНИТЕ ДЕВИЧЕСКИ УЧИЛИЩА И В ДОЛНИЯ КУРС НА ДЕВИЧЕСКИТЕ ГИМНАЗИИ (1897 Г.): ГЕОГРАФИЯ
TEACHING SCIENCE IN THE BULGARIAN SCHOOLS FOR GIRLS (1897): GEOGRAPHY
Книжка 3
ОБУЧЕНИЕ ПО УЧЕБНАТА ДИСЦИПЛИНА „АНАЛИТИЧНА ХИМИЯ“ (КРАТЪК КУРС) ЗА СТУДЕНТИ ОТ НЕХИМИЧЕСКИ СПЕЦИАЛНОСТИ
CHEMISTRY MINOR PROGRAMS: TEACHING AND LEARNING OF ANALYTICAL CHEMISTRY
КЪМ МОДЕРНИЗАЦИЯ НА ПЕДАГОГИКАТА: КРИТИЧЕН ПРЕГЛЕД
Юрий Клисаров, Калина Белчева
ПЪТИЩА ЗА РАЗВИТИЕ НА ПОЗНАВАТЕЛНИЯ ИНТЕРЕС НА УЧЕНИЦИТЕ ПО ПРЕДМЕТА „ЧОВЕКЪТ И ПРИРОДАТА, VІ КЛАС: СТРУКТУРА И ЖИЗНЕНИ ПРОЦЕСИ НА ОРГАНИЗМИТЕ“ В КОНТЕКСТА НА КВАЛИФИКАЦИЯТА НА УЧИТЕЛИ БЕЗ БИОЛОГИЧНО ОБРАЗОВАНИЕ. II.
Мария Бойчева, Росица Давидова
TEACHING AIDS IN PRESENTING THE TOPIC OF „THE PERIODIC TABLE OF ELEMENTS BY DMITRI IVANOVICH MENDELEEV“ AT THE PRIMARY SCHOOL
Milan D. Stojković
ВЪЗМОЖНОСТИ ЗА ФОРМИРАНЕ НА УМЕНИЯ В ОБУЧЕНИЕТО ПО БИОЛОГИЯ
Светлана Ангелова
SIMULATION OF THE FATTY ACID SYNTHASE COMPLEX MECHANISM OF ACTION
M.E.A. Mohammed, Ali Abeer, Fatima Elsamani, O.M. Elsheikh, Abdulrizak Hodow, O. Khamis Haji
FORMING OF CONTENT OF DIFFERENTIAL TEACHING OF CHEMISTRY IN SCHOOL EDUCATION OF UKRAINE
G. Yuzbasheva Kherson Academy of Continuing Education, Ukraine
ИЗСЛЕДВАНЕ НА РАДИКАЛ-УЛАВЯЩА СПОСОБНОСТ
Станислав Станимиров, Живко Велков
Книжка 2
REVERSIBILITY AND DEFINITION OF WORK
Jamil Ahmad
TECHNIQUES OF THE SCHOOL EXPERIMENT IN SCIENCES, FOR BULGARIAN STUDENTS WITH SPECIAL NEEDS
M. Zamfi rov, S. Saeva
ЕКСТРАКЦИОННА СПЕКТРОФОТОМЕТРИЯ НА ЙОННО-АСОЦИИРАНИ КОМПЛЕКСИ
Кирил Б. Гавазов
ИЗРАВНЯВАНЕ НА ОКИСЛИТЕЛНО- РЕДУКЦИОННИ РЕАКЦИИ С ДВЕ СТЕПЕНИ НА СВОБОДА: ИЗСЛЕДВАНЕ НА ОБЛАСТИТЕ ЗА ИЗБОР НА НЕЗАВИСИМИ ПАРАМЕТРИ
Сашка Петкова , Мария Атанасова, Александър Захариев
LEARNING ENVIRONMENT OF UNIVERSITY CHEMISTRY CLASSROOMS IN IRAN
Zahra Eskandari, Nabi.A Ebrahimi
ХРИСТО КОСТОВ – ЖИЗНЕН ПЪТ И НАУЧНА ДЕЙНОСТ
Христо Д. Димитров
Книжка 1
РАЗВИТИЕ НА ЛИЧНОСТНАТА РЕФЛЕКСИЯ НА УЧЕНИЦИТЕ В УЧИЛИЩНОТО ОБУЧЕНИЕ ПО МОЛЕКУЛНА БИОЛОГИЯ, ГЕНЕТИКА И КЛЕТЪЧНОИНЖЕНЕРНИ БИОТЕХНОЛОГИИ
Иса ХАДЖИАЛИ, Теодора КОЛАРОВА
PERSPECTIVES ON TECHNOLOGY ENHANCED LEARNING AND TEACHING FOR AN EXCITING LEARNING EXPERIENCE
B. H. S. THIMMAPPA
COLORFUL EXPERIMENTS FOR STUDENTS: SYNTHESIS OF INDIGO AND DERIVATIVES
Vanessa BIANDA, Jos-Antonio CONSTENLA, Rolf HAUBRICHS, Pierre-Lonard ZAFFALON
ПЪРВАТА КНИГА ПО ХИМИЯ НА БЪЛГАРСКИ ЕЗИК (1871 Г.) – АВТОРИ И ИЗТОЧНИЦИ
Александрия ГЕНДЖОВА
OBSERVING CHANGE IN POTASSIUM ABUNDANCE IN A SOIL EROSION EXPERIMENT WITH FIELD INFRARED SPECTROSCOPY
Mila Ivanova Luleva, Harald van der Werff, Freek van der Meer, Victor Jetten
PERSONAL OR COLLECTIVE KNOWLEDGE: HARRY COLLINS’ KNOWLEDGE NOTIONS OF TACIT KNOWLEDGE AND OF THE INDIVIDUAL AS AN EPISTEMIC PARASITE
Keith S. TABER
ЦАРСКАТА ПЕЩЕРА
Рафаил ПОПОВ
УЧИЛИЩНИ ЛАБОРАТОРИИ И ОБОРУДВАНЕ SCHOOL LABORATORIES AND EQUIPMENT
Учебни лаборатории Илюстрации от каталог на Franz Hugershoff, Лайциг, притежаван от бъдещия
2012 година
Книжка 6
ХИМИЧЕСКО ОБРАЗОВАНИЕ В КОНТЕКСТ. ПРЕДИЗВИКАТЕЛСТВА ПРЕД БЪДЕЩИТЕ УЧИТЕЛИ
Александрия Генджова
ПЪТИЩА ЗА РАЗВИТИЕ НА ПОЗНАВАТЕЛНИЯ ИНТЕРЕС НА УЧЕНИЦИТЕ ПО ПРЕДМЕТА „ЧОВЕКЪТ И ПРИРОДАТА, VІ КЛАС: СТРУКТУРА И ЖИЗНЕНИ ПРОЦЕСИ НА ОРГАНИЗМИТЕ“ В КОНТЕКСТА НА КВАЛИФИКАЦИЯТА НА УЧИТЕЛИ БЕЗ БИОЛОГИЧНО ОБРАЗОВАНИЕ. I.
Мария Бойчева, Росица Давидова
ADDRESING STUDENTS’ MISCONCEPTIONS CONCERNING CHEMICAL REACTIONS AND SYMBOLIC REPRESENTATIONS
Marina I. Stojanovska, Vladimir M. Petruševski, Bojan T. Šoptrajanov
АНАЛИЗ НА ПОСТИЖЕНИЯТА НА УЧЕНИЦИТЕ ОТ ПЕТИ КЛАС ВЪРХУ РАЗДЕЛ „ВЕЩЕСТВА И ТЕХНИТЕ СВОЙСТВА“ ПО ЧОВЕКЪТ И ПРИРОДАТА
Иваничка Буровска, Стефан Цаковски Регионален инспекторат по образованието – Ловеч
SCIENCE TEACHERS’ VIEWS ON NATURE OF SCIENCE: A CASE OF BANGLADESHI SECONDARY SCHOOLS
Muhammad Nur-E-Alam Siddiquee, Hideo Ikeda
PHYTOCHEMISTRY OF TURMERIC: AN OVERVIEW
bizuneh Adinew
ЕКОТОКСИКОЛОГИЯ
Васил Симеонов
ДОБРИ ЛАЗАРОВ – ХИМИК, ПРЕПОДАВАТЕЛ, ПОПУЛЯРИЗАТОР НА НАУКАТА
DOBRI LAZAROV – CHEMIST, EDUCATOR, POPULIZER OF SCIENCE
ЕЛКА ПЕНЧЕВА – СЕМЕЙНА ТРАДИЦИЯ И СОБСТВЕНИ ПОСТИЖЕНИЯ
ELKA PENCHEVA – FAMILY TRADITION AND OWN ACHIEVEMENTS
АЛЕКСЕЙ ШЕЛУДКО И ПРИНОСЪТ МУ КЪМ ОБЛАСТТА НА ЕЛЕКТРОКРИСТАЛИЗАЦИЯТА
Александър Милчев
ПРОФ. МЕДОДИЙ ПОПОВ ЗА НАУКАТА И НАУЧНАТА ДЕЙНОСТ (1920 Г.)
Проф. Методий Попов (1881-1954) Госпожици и Господа студенти,
Книжка 5
КАК ДА ИЗМЕРИМ ПОСТИГНАТИТЕ РЕЗУЛТАТИ П О КОНКРЕТНА ОБР А ЗОВАТЕЛНА ЦЕЛ?
HOW TO MEASURE THE SCHOOL OUTCOME (ON THE EXAMPLE OF A SPECIFIC EDUCATIONAL GOAL)
ПРЕДСТАВИТЕ ЗА СВЕТА: ОБЯСНЕНИЕТО В ОБУЧЕНИЕТО ПО ПРИРОДНИ НАУКИ И СВЕТОГЛЕДА
Йорданка Стефанова, Мария Миневска
КОНЦЕПТУАЛНА СХЕМА НА УЧИЛИЩНИЯ КУРС П О ХИМИЯ – МАКР О СКОПСКИ ПОДХОД
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
ROLE OF ULTRASONIC WAVES TO STUDY MOLECULAR INTERACTIONS IN AQUEOUS SOLUTION OF DICLOFENAC SODIUM
Sunanda S. Aswale, Shashikant R. Aswale, Aparna B. Dhote Lokmanya Tilak Mahavidyalaya, INDIA Nilkanthrao Shinde College, INDIA
SIMULTANEOUS ESTIMATION OF IBUPROFEN AND RANITIDINE HYDROCHLORIDE USING UV SPECTROPHOT O METRIC METHOD
Jadupati Malakar, Amit Kumar Nayak Bengal College of Pharmaceutical Sciences and Research, INDIA
A NEW FORMAL GEOMETRICAL METHOD FOR BALANCING CONTINUUM CLASSES O F CHEMICAL REACTIONS
Ice B. Risteski
GAPS AND OPPORTUNITIES IN THE USE OF REMOTE SENSING FOR SOIL EROSION ASSESSMENT
Mila Ivanova Luleva, Harald van der Werff, Freek van der Meer, Victor Jetten
РАДИОХИМИЯ И АРХЕОМЕТРИЯ: ПРО Ф. ДХН ИВЕЛИН КУЛЕВ RADIOCHEMISTRY AND ARCHEOMETRY: PROF. IVELIN KULEFF, DSc
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
Книжка 4
TEACHING THE CONSTITUTION OF MATTER
Małgorzata Nodzyńska, Jan Rajmund Paśko
СЪСИРВАЩА СИСТЕМА НА КРЪВТА
Маша Радославова, Ася Драгоева
CATALITIC VOLCANO
CATALITIC VOLCANO
43-ТА МЕЖДУНАРОДНА ОЛИМПИАДА ПО ХИМИЯ
Донка ТАШЕВА, Пенка ЦАНОВА
NEW VERY HARD PROBLEMS OF BALANCING CHEMICAL REACTIONS
Ice B. Risteski
ЮБИЛЕЙ: ПРОФ. ДХН БОРИС ГЪЛЪБОВ JUBILEE: PROF. DR. BORIS GALABOV
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
ПЪРВИЯТ ПРАВИЛНИК ЗА УЧЕБНИЦИТЕ (1897 Г.)
Чл. 1. Съставянето и издаване на учебници се предоставя на частната инициа- тива. Забележка: На учителите – съставители на учебници се запрещава сами да разпродават своите учебници. Чл. 2. Министерството на народното просвещение може да определя премии по конкурс за съставяне на учебници за горните класове на гимназиите и специ- алните училища. Чл. 3. Никой учебник не може да бъде въведен в училищата, ако предварително не е прегледан и одобрен от Министерството на народното просвещение. Чл.
JOHN DEWEY: HOW WE THINK (1910)
John Dewey (1859 – 1952)
ИНФОРМАЦИЯ ЗА СПЕЦИАЛНОСТИТЕ В ОБЛАСТТА НА ПРИРОДНИТЕ НАУКИ В СОФИЙСКИЯ УНИВЕРСИТЕТ „СВ. КЛИМЕНТ ОХРИДСКИ“ БИОЛОГИЧЕСКИ ФАКУЛТЕТ
1. Биология Студентите от специалност Биология придобиват знания и практически умения в областта на биологическите науки, като акцентът е поставен на организмово равнище. Те се подготвят да изследват биологията на организмите на клетъчно- организмово, популационно и екосистемно ниво в научно-функционален и прило- жен аспект, с оглед на провеждане на научно-изследователска, научно-приложна, производствена и педагогическа дейност. Чрез широк набор избираеми и факул- тативни курсове студентите
Книжка 3
УЧЕБНО-ПОЗНАВАТЕЛНИ ЗАДАЧИ ЗА ФОРМИРАНЕ И РАЗВИТИЕ НА КОМПЕТЕНТНОСТ ЗА МОДЕЛИРАНЕ В ОБУЧЕНИЕТО ПО ХИМИЯ И ОПАЗВАНЕ НА ОКОЛНАТА СРЕДА
Николай Цанков
МОДЕЛ НА СПЕЦИАЛИСТА УЧИТЕЛ ПО БИОЛОГИЯ – ПРОФЕСИОНАЛЕН ПРОФИЛ И СТАНДАРТИ ЗА ПОДГОТОВКА
Наташа Цанова, Надежда Райчева
АНАЛИЗ НА РЕЗУЛТАТИТЕ ОТ ВЪНШНОТО ОЦЕНЯВАНЕ ПО „ЧОВЕКЪТ И ПРИРОДАТА” ЗА 4. КЛАС В СПЕЦИАЛНИТЕ И ОЗДРАВИТЕЛНИ УЧИЛИЩА В БЪЛГАРИЯ
Милен Замфиров
УЧИТЕЛИТЕ ПО ПРИРОДНИ НАУКИ – ЗА КОНСТРУКТИВИСТКАТА УЧЕБНА СРЕДА В БЪЛГАРСКОТО УЧИЛИЩЕ
Адриана Тафрова-Григорова, Милена Кирова, Елена Бояджиева
PREPARATION AND CHARACTERIZATION OF ACTIVATED CARBON DERIVED FROM RUBBER SEED COAT
Olugbenga Solomon Bello, Mohd Azmier Ahmad
МЕТОД ЗА ИЗМЕРВАНЕ НА СРЕДНОТО СЛЪНЧЕВО ВРЕМЕ С ЦИЛИНДРИЧЕН СЛЪНЧЕВ ЧАСОВНИК
Звездо Костов Христов
ПОВИШАВАНЕ ИНТЕРЕСА КЪМ ИСТОРИЯТА НА ХИМИЧНИТЕ ЗНАНИЯ И ПРАКТИКИ ПО БЪЛГАРСКИТЕ ЗЕМИ
Людмила Генкова, Свобода Бенева Българско дружество за химическо образование и история и философия на химията
НАЧАЛО НА ПРЕПОДАВАНЕТО НА УЧЕБЕН ПРЕДМЕТ ХИМИЯ В АПРИЛОВОТО УЧИЛИЩЕ В ГАБРОВО
Мария Николова Национална Априловска гимназия – Габрово
ПРИРОДОНАУЧНОТО ОБРАЗОВАНИЕ В БЪЛГАРИЯ – ФОТОАРХИВ
В един дълъг период от време гимназиалните учители по математика, физика, химия и естествена
Книжка 2
„МАГИЯТА НА ХИМИЯТА“ – ВЕЧЕР НА ХИМИЯТА В ЕЗИКОВА ГИМНАЗИЯ „АКАД. Л. СТОЯНОВ“ БЛАГОЕВГРАД
Стефка Михайлова Езикова гимназия „Акад. Людмил Стоянов“ – Благоевград
НАУЧЕН ТЕАТЪР – ВАРИАНТ ЗА ИЗЯВА НА ТАЛАНТЛИВИТЕ УЧЕНИЦИ И ПОВИШАВАНЕ ИНТЕРЕСА КЪМ ПРИРОДНИТЕ НАУКИ ENHANCEMENT THE INTEREST OF STUDENTS TO SCIENCE THROUGH DRAMA ACTIVITIES
Мария Николова Национална Априловска гимназия – гр. Габрово
МЕЖДУНАРОДНАТА ГОДИНА НА ХИМИЯТА 2011 В ПОЩЕНСКИ МАРКИ
Б. В. Тошев Българско дружество за химическо образование и история и философия на химията
ОБЩИ УМЕНИЯ И КОМПЕТЕНТНОСТИ ЗА ПРОФЕСИОНАЛНАTA РЕАЛИЗАЦИЯ НА ВИПУСКНИЦИ НА ХИМИЧЕСКИЯ ФАКУЛТЕТ ПРИ СОФИЙСКИЯ УНИ ВЕРСИТЕТ „СВ. КЛИМЕНТ ОХРИДСКИ“
Александрия ГЕНДЖОВА, Александра КАМУШЕВА
ПОРТФОЛИОТО – СРЕДСТВО ЗА МОНИТОРИНГ НА ПРОФЕСИОНАЛНИТЕ КОМПЕТЕНЦИИ НА УЧИТЕЛИТЕ ПО ПРИРОДНИ НАУКИ
Петинка Р. Галчева, Антоанета И. Хинева
A NEW ALGEBRA FOR BALANCING SPECIAL CHEMICAL REACTIONS
Ice B. Risteski
RE-EXAMINING TRADITIONAL AND ROTATIONAL CANONICAL PARTITION FUNCTIONS FOR UNDERGRADUATE PHYSICAL CHEMISTRY: EXACT AND INSIGHTFUL VIEWS
Mohamad Toutounji
АКАДЕМИК ДИМИТЪР ИВАНОВ – ЖИЗНЕН ПЪТ И НАУЧНО ДЕЛО
Христо Иванов
КОМПЕТЕНТНОСТИ И ВИЖДАНИЯ НА УЧИТЕЛИ ЗА ПРИЛОЖЕНИЕ НА ЕЛЕКТРОННОТО ОБУЧЕНИЕ ПО ПРИРОДНИ НАУКИ В СРЕДНОТО УЧИЛИЩЕ
Милена Кирова, Елена Бояджиева, Румяна Пейчева-Форсайт
ПОМАГАЛО ЗА ДОКТОРАНТИ В НАУКАТА ЗА ОБРАЗОВАНИЕТО
A GUIDE FOR DOCTORAL STUDENTS IN THE SCIENCE OF EDUCATION
АЛГОЛОГИЯ
ALGOLOGY
ЗА ПРИРОДНИТЕ НАУКИ И ЗА ПРАКТИКУМА ПО ФИЗИКА (Иванов, 1926)
Бурният развой на естествознанието във всичките му клонове през XIX –ия век предизвика дълбоки промени в мирогледа на културния свят, в техниката и в индустрията, в социалните отношения и в държавните интереси. Можем ли днес да си представим един философ, един държавен мъж, един обществен деец, един индустриалец, просто един културен човек, който би могъл да игнорира придобив- ките на природните науки през последния век. Какви ужасни катастрофи, какви социални сътресения би сполетяло съвре
Книжка 1
ПРИРОДНИТЕ НАУКИ В НАУКАТА ЗА ОБРАЗОВАНИЕТО
Б. В. Тошев
МЕДИЦИНАТА ПРЕЗ ПОГЛЕДА НА ТРИ НАУКИ, ТРИМА ПРЕПОДАВАТЕЛИ И ЕДИН КЛАС
Ю. Белчева, А. Стамболджиева
ВИЗУАЛИЗАЦИЯ НА ТОПЛИННИ ЯВЛЕНИЯ ПОСРЕДСТВОМ PHYSLETS®
Клавдий Тютюлков
ADAPTATION STUDY OF MOTIVATION TOWARD SCIENCE LEARNING QUESTIONNAIRE FOR ACADEMICALLY ADVANCED SCIENCE STUDENTS
Mustafa Serdar Köksal
ВЕРБАЛНИТЕ АСОЦИАЦИИ НА БЪЛГАРСКИ ТИЙНЕЙДЖЪРИ ЗА ВЕЩЕСТВО
Йорданка Димова, Калина Камарска
МИСЛОВНИ УМЕНИЯ НА ВИСОКО И НИСКО НИВО, ЗАЛОЖЕНИ В БЪЛГАРСКИ И КАНАДСКИ УЧЕБНИ ПРОГРАМИ
Александрия Генджова
A SIMPLE EXPLANATION FROM THE SIGN OF r- VALUE FOR THE KIND OF CHARGE THAT DEVELOPS IN THE INTERMEDIATE OR THE TRANSITION STATE OF A REACTION SERIES: A ONE-HOUR PHYSICAL-ORGANIC CHEMISTRY GRADUATE CLASSROOM LECTURE
R. Sanjeev, V. Jagannadham, R. Veda Vrath
MURPHY’S LAW IN CHEMISTRY
Milan D. Stojković
42-рa МЕЖДУНАРОДНА ОЛИМПИАДА ПО ХИМИЯ
Донка Ташева, Пенка Цанова
SOLUBILITY AND DISSOLUTION ENHANCEMENT OF IBUPROFEN BY SOLID DISPERSION TECHNIQUE USING PEG 6000-PVP K 30 COMBINATION CARRIER
M. Saquib Hasnain, Amit Kumar Nayak
ИСТОРИЯ НА ФИЗИКАТА HISTORY OF PHYSICS
Б. В. Тошев
ГЕОГРАФИЯ И ПЪТЕШЕСТВИЯ GEOGRAPHY AND JOURNEYS
В. Б. Тошев
СЕМЕЙНИ УЧЕНИЧЕСКИ ВЕЧЕРИНКИ
Семейството трябва да познава училишето и училишето трябва да познава семейството. Взаимното познанство се налага от обстоятелството, че те, макар и да са два различни по природата си фактори на възпитанието, преследват една и съща проста цел – младото поколение да бъде по-умно, по-нравствено, физически по-здраво и по-щастливо от старото – децата да бъдат по-щастливи от родителите
АКАДЕМИК РОСТИСЛАВ КАИШЕВ – ЖИВОТ, ПОСВЕТЕН НА НАУКАТА
Александър Милчев, Стоян Стоянов